Posted on: April 8, 2025 | Reading time: 18 minutes | Word count: 3831 words | Author: Dang Duong Minh Nhat
Hello and welcome back to Part 2 of this cryptography series! If you haven’t already, I highly recommend reading Part 1 before diving in, as it lays the groundwork for everything we’ll cover here.
In this post, we’ll explore the concept of computational encryption schemes, dig into the formal definition of semantic security, and analyze a specific type of attack known as a message recovery attack. Most importantly, we’ll prove a fundamental result: that semantic security inherently protects against message recovery—and we’ll do it using one of cryptography’s most powerful proof techniques: security reductions.
Let’s get started.
Computational Ciphers and Semantic Security
As we already know from Shannon’s theorem (Theorem 4 in the blog post Cryptography 1), the only way to achieve perfect secrecy is to use a key whose length is equal to that of the message. However, this requirement is impractical in many real-world scenarios. Ideally, we would like to encrypt long messages (e.g., documents that are several megabytes in size) using a short key (e.g., only a few hundred bits).
The only way to circumvent Shannon’s theorem is to relax our security requirements. We do so by restricting our attention to computationally bounded adversaries — attackers in the real world who can only perform computations within reasonable time and memory constraints on actual hardware. This shift in perspective leads to a weaker, yet still meaningful, definition of security called semantic security.
Moreover, our new security definition is designed to be flexible: it allows encryption schemes with variable-length message spaces to still be considered secure, as long as they leak no useful information about the plaintext message to the adversary — other than possibly the length of the message. Since our focus is now on practical security rather than information-theoretic guarantees, we additionally require that both the encryption and decryption algorithms be efficient, i.e., computable in polynomial time.
Definition of Computational Ciphers
A computational cipher $\mathcal{E} = (E, D)$ consists of a pair of efficient algorithms $E$ and $D$:
- The encryption algorithm $E$ takes a key $k$ and a message $m$ as input, and outputs a ciphertext $c$.
- The decryption algorithm $D$ takes a key $k$ and a ciphertext $c$ as input, and outputs the message $m$.
The key belongs to a finite key space $\mathcal{K}$, the messages to a finite message space $\mathcal{M}$, and the ciphertexts to a finite ciphertext space $\mathcal{C}$. Similar to Shannon’s ciphers, we say that $\mathcal{E}$ is defined over the triple $\left( \mathcal{K}, \mathcal{M}, \mathcal{C} \right)$.
Probabilistic Encryption
We say that the encryption algorithm $E$ is probabilistic, meaning that for a fixed key $k$ and message $m$, the output of $E(k, m)$ can vary across multiple executions. To emphasize the randomness in the encryption process, we write
$$ c \xleftarrow{R} E(k, m) $$
which denotes executing $E(k, m)$ and assigning its (random) output to variable $c$.
Similarly, to represent selecting a random key from the key space $\mathcal{K}$, we write
$$ k \xleftarrow{R} \mathcal{K} $$
to denote that $k$ is chosen uniformly at random from $\mathcal{K}$.
Although the decryption algorithm could, in principle, be probabilistic, we will not focus on that here (this possibility will be revisited later). Therefore, we consider only encryption schemes with deterministic decryption algorithms. Nevertheless, we sometimes allow the decryption algorithm to return a special value (distinct from any valid message) to indicate a decryption error.
Correctness of Decryption
Since the encryption algorithm is probabilistic, it may output different ciphertexts for the same key $k$ and message $m$ on different executions. However, every ciphertext produced must decrypt correctly back to the original message. We formalize this requirement as follows: for every $k \in \mathcal{K}$ and every $m \in \mathcal{M}$, if
$$ c \xleftarrow{R} E(k, m), \quad m’ \leftarrow D(k, c), $$
then it must hold that
$$ \Pr\left[ D(k, c) = m \mid c \xleftarrow{R} E(k, m) \right] = 1. $$
From now on, whenever we refer to an encryption scheme, we implicitly mean a computational cipher as defined above. If the encryption algorithm is deterministic, we refer to the scheme as a deterministic cipher.
Comparison with Shannon Ciphers
Note that every deterministic cipher is also a Shannon cipher. However, a computational cipher is not necessarily a Shannon cipher (if its encryption algorithm is probabilistic), and conversely, a Shannon cipher is not necessarily a computational cipher (if it lacks efficient encryption or decryption algorithms). Let’s revisit some examples from Cryptography 1:
- The one-time pad and variable-length one-time pad are both deterministic ciphers, since their encryption and decryption can be implemented easily using efficient deterministic algorithms.
- The substitution cipher is also a deterministic cipher, as long as the size of the alphabet $\Sigma$ is not too large. In practice, a key (a permutation of $\Sigma$) is often represented as an array indexed by the characters in $\Sigma$, requiring $O(|\Sigma|)$ storage. This is only practical when $\Sigma$ is of reasonable size.
- The additive one-time pad is likewise a deterministic cipher, since both encryption and decryption operations are efficient. For large values of $n$, special-purpose software may be needed to perform arithmetic over large integers.
Definition of Semantic Security
We now delve deeper into the definition of semantic security. Consider a deterministic encryption scheme $\mathcal{E} = (E, D)$ defined over the tuple $(\mathcal{K}, \mathcal{M}, \mathcal{C})$. Recall Theorem 2 on perfect secrecy from Cryptography 1, which states:
$$ \Pr[\phi(E(\mathbf{k}, m_0))] = \Pr[\phi(E(\mathbf{k}, m_1))] $$
where $\mathbf{k}$ is a random variable uniformly sampled from the key space $\mathcal{K}$.
Instead of requiring these two probabilities to be exactly equal, we now relax the condition and only require them to be very close, that is:
$$ \left| \Pr[\phi(E(\mathbf{k}, m_0))] - \Pr[\phi(E(\mathbf{k}, m_1))] \right| \leq \epsilon $$
for some small (possibly negligible) value $\epsilon$.
However, this condition is still too strict. Rather than requiring it to hold for all choices of messages $m_0, m_1$ and functions $\phi$, we only require it to hold for:
- message pairs $m_0, m_1$ generated by efficient algorithms, and
- functions $\phi$ that are also efficiently computable (these algorithms may be probabilistic).
For example, suppose that even using the most powerful algorithms running on 10,000 machines in parallel for 10 years, the inequality above still holds with $\epsilon = 2^{-100}$. In such a case, the scheme may not be perfectly secure, but we may still consider it to be secure in practice.
Furthermore, this relaxed definition of semantic security also addresses issues such as the variable-length one-time pad, which fails to achieve perfect secrecy as shown in Cryptography 1. Our goal is to have a flexible definition that can still regard such schemes as secure—as long as they leak no information about the message except its length.
Let us now proceed to formalize the notion of semantic security through an attack game involving two parties:
- the challenger, and
- the adversary.
We define different attack games to capture various levels of security. In these games:
- The challenger follows a fixed protocol.
- The adversary may employ any strategy, as long as it is computationally efficient.
- The two parties interact via a defined protocol, and in the end, the adversary outputs a guess.
Each attack game defines a probability space, from which we compute the adversary’s advantage based on the probability of certain events. Some games are modeled using two separate experiments:
- In both experiments, the adversary follows the same strategy.
- However, the challenger’s behavior differs in each experiment.
Specifically:
- The adversary selects two messages $m_0, m_1$ of equal length and sends them to the challenger.
- The challenger performs one of the following two experiments:
- Experiment 0: Encrypts $m_0$ using a randomly chosen key.
- Experiment 1: Encrypts $m_1$ using a randomly chosen key.
- The challenger returns the resulting ciphertext $c$ to the adversary.
- The adversary analyzes $c$ and attempts to guess which message was encrypted, outputting a bit $\hat{b} \in \left\lbrace 0, 1 \right\rbrace$.
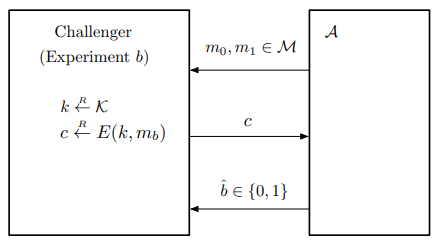
Let’s now define the Semantic Security Game formally. Given an encryption scheme $\mathcal{E} = (E, D)$ defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$ and an adversary $\mathcal{A}$, we define two experiments: Experiment 0 and Experiment 1. For $b \in \left\lbrace 0, 1 \right\rbrace$, Experiment b is defined as follows:
- The adversary chooses two messages $m_0, m_1 \in \mathcal{M}$ of equal length and sends them to the challenger.
- The challenger performs the following steps:
- Samples a random key: $k \xleftarrow{R} \mathcal{K}$
- Encrypts message $m_b$: $c \xleftarrow{R} E(k, m_b)$
- Sends the ciphertext $c$ to the adversary
- The adversary observes $c$ and outputs a guess bit $\hat{b} \in \left\lbrace 0, 1 \right\rbrace$.
To visualize this, refer to the diagram below:
Definition of Adversary’s Advantage
Let $W_b$ denote the event that adversary $\mathcal{A}$ outputs $\hat{b} = 1$ in Experiment b. Then, the advantage of $\mathcal{A}$ in breaking the semantic security of the encryption scheme $\mathcal{E}$ is defined as:
$$ \mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}] := \left| \Pr[W_0] - \Pr[W_1] \right|. $$
In the above attack game, the events $W_0$ and $W_1$ are defined over a probability space that depends on:
- The random choice of the key $k$.
- The internal randomness (if any) of the encryption algorithm.
- The randomness (if any) used by the adversary.
The value $\mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}]$ always lies in the interval $[0,1]$. If this value is very small, it indicates that the adversary cannot distinguish between the ciphertexts of $m_0$ and $m_1$, thereby preserving the semantic security of the encryption scheme.
Definition (Semantic Security)
An encryption scheme $\mathcal{E}$ is said to be semantically secure if for every efficient adversary $\mathcal{A}$, the value $\mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}]$ is negligible. This definition, however, is not yet fully rigorous, since the notions of “messages of the same length,” “efficient adversary,” and “negligible function” have not been precisely defined. We will revisit these notions later.
Assume that the adversary $\mathcal{A}$ in the Semantic Security Attack Game is deterministic. Then:
- $\mathcal{A}$ chooses two messages $m_0, m_1$ deterministically.
- $\mathcal{A}$ evaluates a predicate $\phi$ on the ciphertext $c$ and outputs $1$ if true, and $0$ otherwise.
Semantic security requires that the value $\epsilon$ in the inequality
$$ \left| \Pr[\phi(E(k, m_0))] - \Pr[\phi(E(k, m_1))] \right| \leq \epsilon $$
is negligible.
If $\mathcal{A}$ is a randomized algorithm, we can model it as follows:
- Sample a random value $r$ from some suitable distribution.
- Determine two messages $m_0^{(r)}$, $m_1^{(r)}$ based on $r$.
- Evaluate a predicate $\phi^{(r)}$ on $c$, which may also depend on $r$.
In this case, semantic security requires that the value $\epsilon$ in the inequality above (now applied to $m_0^{(r)}, m_1^{(r)}, \phi^{(r)}$) is negligible—where the probability is taken over the randomness of both the encryption key and the random value $r$.
We now make several observations about the requirement that the two messages $m_0$ and $m_1$ selected by the adversary in the Semantic Security Attack Game must have equal length.
First, the concept of “length” for a message depends on the message space $\mathcal{M}$.
- When defining a message space, we also need to define a function that assigns a non-negative integer length to each message.
- In many practical cases, this is straightforward. For example, in $\left\lbrace 0,1 \right\rbrace^{\leq L}$, the length of a message $m \in \left\lbrace 0,1 \right\rbrace^{\leq L}$ is simply the number of bits it contains, denoted $|m|$.
- However, for generality, we leave the notion of length abstract, without assigning a fixed rule.
- In certain message spaces, the notion of length may not exist, in which case we can assume that all messages have length zero.
Second, the requirement that $m_0$ and $m_1$ have the same length ensures that an adversary cannot trivially break the encryption by distinguishing ciphertexts based solely on message lengths.
- Without this requirement, an encryption scheme might be considered insecure simply because it leaks the message length.
- This reflects the reality that most practical encryption schemes do allow leakage of message length, but they should not leak any content of the message.
Let us revisit the variable-length one-time pad example from Cryptography 1, where leakage of message length can have serious consequences in some applications. However, since there is no general solution to hide message lengths, most real-world schemes (e.g., TLS) do not attempt to conceal this information. This has led to practical attacks, and in some sensitive contexts, ciphertext length leakage can be a severe security risk.
Nonetheless, semantic security is typically assumed to be independent of message length, so let us consider the following example. Suppose $\mathcal{E}$ is a deterministic encryption scheme with perfect security. Then it is easy to see that for all adversaries $\mathcal{A}$, efficient or otherwise, we have:
$$ \mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}] = 0. $$
This follows almost immediately from Theorem 2 in Cryptography 1 (with the minor caveat that $\mathcal{A}$ in the semantic security game may be randomized, but this is easy to address). Therefore, the encryption scheme $\mathcal{E}$ is semantically secure. Specifically:
- If $\mathcal{E}$ is the one-time pad, then $\mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}] = 0$ for all $\mathcal{A}$. In other words, the one-time pad is semantically secure.
- As noted earlier, since the definition of semantic security assumes that the adversary cannot break the scheme by distinguishing ciphertext lengths, it is also easy to show that if $\mathcal{E}$ is the variable-length one-time pad, then again $\mathtt{SS}\text{adv}[\mathcal{A},\mathcal{E}] = 0$ for all $\mathcal{A}$. That is, the variable-length one-time pad is also semantically secure.
Before proceeding, let me first clarify two important notions: “efficient” and “negligible”. While we will study these concepts more formally in later sections, here is a simple intuitive explanation:
A function is negligible if its value is so small that it can be considered practically zero. For example, consider the value $2^{-100}$. If the probability that you spontaneously combust in the next year is $2^{-100}$, then you would not worry about that event any more than you would worry about an event with probability $0$.
An efficient adversary refers to one that runs in a “reasonable” amount of time. Formally, its running time is bounded by a polynomial function of the input size. In other words, it cannot take more than a polynomial number of steps in the size of its input.
Rather than diving into technical details, let us walk through an example that illustrates how this definition is used to analyze the security of a larger system that employs a semantically secure encryption scheme.
Message Recovery Attack
As our first example, we consider a Message Recovery (MR) attack, in which an adversary is given a ciphertext corresponding to a random message and attempts to recover the original message with significantly better probability than random guessing, that is, better than $1 / |\mathcal{M}|$. Clearly, any reasonable notion of security should prevent such attacks—including semantic security.
Although this may seem obvious (after all, if the adversary cannot distinguish between $m_0$ and $m_1$, it certainly cannot recover a random message), we will provide a formal proof. This will also serve as a detailed example of the technique called security reduction, which is the primary method used to argue the security of cryptographic systems.
The core idea of a security reduction is as follows: suppose there exists an efficient adversary $\mathcal{A}$ that succeeds in a message recovery attack against an encryption scheme $\mathcal{E}$. Then we can construct an efficient adversary $\mathcal{B}$ that breaks the semantic security of $\mathcal{E}$. Since semantic security implies that no such efficient adversary $\mathcal{B}$ can exist, it follows that no such $\mathcal{A}$ exists either.
As in semantic security, the attack is modeled by an interaction between a challenger and an adversary, forming a security game we call the Message Recovery game. The game proceeds as follows for a symmetric encryption scheme $\mathcal{E} = (E, D)$ defined over message space $\mathcal{M}$, key space $\mathcal{K}$, and ciphertext space $\mathcal{C}$:
The challenger samples a message $m \xleftarrow{R} \mathcal{M}$, a key $k \xleftarrow{R} \mathcal{K}$, and computes the ciphertext $c \xleftarrow{R} E(k, m)$. The ciphertext $c$ is sent to the adversary.
The adversary outputs a message guess $\hat{m} \in \mathcal{M}$.
Let $W$ denote the event that $\hat{m} = m$, i.e., the adversary correctly recovers the message. We say that $\mathcal{A}$ wins the game if $W$ occurs. The message recovery advantage of $\mathcal{A}$ against scheme $\mathcal{E}$ is defined as:
$$ \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}] := \left| \Pr[W] - \frac{1}{|\mathcal{M}|} \right|. $$
Definition: Message Recovery Security
An encryption scheme $\mathcal{E}$ is said to be secure against message recovery attacks if, for all efficient adversaries $\mathcal{A}$, the message recovery advantage $\texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]$ is a negligible function in the security parameter. That is, the scheme is secure if every efficient adversary has only negligible advantage over random guessing.
This leads us to the following theorem:
Theorem 1. Let $\mathcal{E} = (E, D)$ be an encryption scheme defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$. If $\mathcal{E}$ is semantically secure, then $\mathcal{E}$ is also secure against message recovery attacks.
Proof. Suppose $\mathcal{E}$ is semantically secure. Our goal is to prove that $\mathcal{E}$ is also secure against message recovery. That is, we must show that for any efficient adversary $\mathcal{A}$, the message recovery advantage $\texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]$ is negligible.
Let:
- $p = \Pr[\mathcal{A} \text{ wins the MR game}]$,
- $|\mathcal{M}|$ be the size of the message space.
Then:
$$ \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}] = \left| p - \frac{1}{|\mathcal{M}|} \right|. $$
We now construct an efficient adversary $\mathcal{B}$ for the semantic security game such that:
$$ \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}] \leq \texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}] \tag{1} $$
Since $\mathcal{E}$ is semantically secure and $\mathcal{B}$ is efficient, we know that $\texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}]$ is negligible, and hence so is $\texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]$.
We treat $\mathcal{A}$ as a black-box and build $\mathcal{B}$ as follows:
$\mathcal{B}$ selects two random messages $m_0, m_1 \in \mathcal{M}$ and submits them to its semantic security challenger.
The challenger returns a ciphertext $c = E(k, m_b)$ where $b \xleftarrow{R} \left\lbrace 0, 1 \right\rbrace$ is random.
$\mathcal{B}$ forwards $c$ to $\mathcal{A}$, pretending it was generated in the MR game.
$\mathcal{A}$ returns a message guess $\hat{m} \in \mathcal{M}$.
$\mathcal{B}$ outputs:
- $\hat{b} = 1$ if $\hat{m} = m_1$,
- $\hat{b} = 0$ otherwise.
This completes the construction of $\mathcal{B}$. Note that the running time of $\mathcal{B}$ is essentially the same as $\mathcal{A}$, since $\mathcal{B}$ simply invokes $\mathcal{A}$ as a subroutine. Now we analyze the advantage of $\mathcal{B}$ in the semantic security game.
Let:
- $p_1 = \Pr[\mathcal{B} \text{ outputs } \hat{b} = 1 \mid c = E(k, m_1)] = \Pr[\hat{m} = m_1] = p$,
- $p_0 = \Pr[\mathcal{B} \text{ outputs } \hat{b} = 1 \mid c = E(k, m_0)] = \Pr[\hat{m} = m_1] = \frac{1}{|\mathcal{M}|}$.
Because when $c = E(k, m_1)$, the adversary $\mathcal{A}$ receives the ciphertext from $\mathcal{B}$ and attempts to recover the original message. The probability that $\mathcal{A}$ correctly outputs $m_1$ is exactly the probability of winning in the message recovery game, that is,
$$ p_1 = \Pr[\hat{m} = m_1] = p. $$
On the other hand, when the ciphertext is an encryption of $m_0$, then $\mathcal{A}$ receives a ciphertext corresponding to $m_0$, with no information whatsoever about $m_1$. In this case, $\mathcal{A}$’s attempt to guess $m_1$ amounts to a blind guess. Therefore,
$$ p_0 = \Pr[\hat{m} = m_1] = \frac{1}{\left|\mathcal{M}\right|}. $$
Then:
$$ \texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}] = |p_1 - p_0| = \left| p - \frac{1}{|\mathcal{M}|} \right| = \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]. $$
This shows that the inequality (1) holds, and in fact, equality is achieved in this case. However, for the purpose of the reduction, the inequality alone is sufficient.
You should make sure you understand the logic of this proof, as this type of argument will be used repeatedly throughout this series. Let us now review the key parts of the proof, and present an alternative perspective to think about it.
At the heart of the proof lies the following proposition: for every efficient message recovery adversary $\mathcal{A}$ against $\mathcal{E}$ in the Message Recovery Attack Game, there exists an efficient semantic security adversary $\mathcal{B}$ against $\mathcal{E}$ in the Semantic Security Attack Game such that:
$$ \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}] \leq \texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}] \tag{2} $$
Our goal is to prove that if $\mathcal{E}$ is semantically secure, then it is also secure against message recovery.
In the proof above, we argued that if $\mathcal{E}$ is semantically secure, then the right-hand side of inequality $(2)$ must be negligible. This implies that the left-hand side must also be negligible. Since this holds for every efficient adversary $\mathcal{A}$, we conclude that $\mathcal{E}$ is secure against message recovery.
An alternative approach to proving the theorem is to use contrapositive reasoning:
If $\mathcal{E}$ is not secure against message recovery, then $\mathcal{E}$ is not semantically secure.
Specifically, suppose that $\mathcal{E}$ is not message recovery secure. This means that there exists an efficient adversary $\mathcal{A}$ whose message recovery advantage is non-negligible. Using $\mathcal{A}$, we construct an efficient adversary $\mathcal{B}$ such that inequality $(2)$ holds. Since $\texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]$ is non-negligible, and by $(2)$ we have $\texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}] \geq \texttt{MR}\text{adv}[\mathcal{A}, \mathcal{E}]$, it follows that $\texttt{SS}\text{adv}[\mathcal{B}, \mathcal{E}]$ is also non-negligible. Hence, $\mathcal{E}$ is not semantically secure. In short:
To prove that semantic security implies message recovery security, it suffices to show how to convert a message recovery adversary into a semantic security adversary.
It is worth emphasizing that the adversary $\mathcal{B}$ constructed in the proof uses $\mathcal{A}$ merely as a black box. In fact, most constructions we will see later follow this template: $\mathcal{B}$ acts as a wrapper around $\mathcal{A}$, providing a simple and efficient communication interface between $\mathcal{B}$’s challenger and a single execution of $\mathcal{A}$.
We say that the computational cost of the interface (the data exchanged between $\mathcal{B}$ and $\mathcal{A}$) does not depend on the computational complexity of $\mathcal{A}$. However, in some cases this cannot be completely avoided. For example, if the attack game allows $\mathcal{A}$ to issue multiple queries to the challenger, then the more queries there are, the more work the interface needs to perform. That said, the workload should depend only on the number of queries, and not on the runtime of $\mathcal{A}$.
Thus, we define $\mathcal{B}$ to be an elementary wrapper around $\mathcal{A}$ if it is constructed in this way, with an efficient interface interacting with $\mathcal{A}$. Key properties of this notion include:
- If $\mathcal{B}$ is an elementary wrapper around $\mathcal{A}$, and $\mathcal{A}$ is efficient, then $\mathcal{B}$ is also efficient.
- If $\mathcal{C}$ is an elementary wrapper around $\mathcal{B}$, and $\mathcal{B}$ is an elementary wrapper around $\mathcal{A}$, then $\mathcal{C}$ is an elementary wrapper around $\mathcal{A}$.
These concepts will be presented more formally in the future.
In this blog, we clarified the connection between semantic security and resistance against message recovery attacks. By employing a security reduction technique, we demonstrated that any encryption scheme achieving semantic security must also thwart any efficient adversary attempting to recover the original message from a ciphertext.
This proof exemplifies a fundamental mindset in modern cryptography: proving that stronger security notions imply weaker ones, using precise reductions. Specifically, we constructed a wrapper adversary that leverages a message recovery attacker as a black-box to break semantic security.
This style of argument—black-box reduction via adversary wrapping—will appear repeatedly throughout this series, serving as a core proof technique. Understanding the logic of this reduction not only solidifies our grasp of semantic security but also lays the groundwork for analyzing more advanced security notions in future posts.
References
- Dan Boneh and Victor Shoup. A Graduate Course in Applied Cryptography. Retrieved from https://toc.cryptobook.us/
Connect with Me
Connect with me on Facebook, LinkedIn, via email at dangduongminhnhat2003@gmail.com, GitHub, or by phone at +84 829 258 815.