Posted on: August 5, 2025 | Reading time: 16 minutes | Word count: 3376 words | Author: Dang Duong Minh Nhat
Hello everyone, and welcome back to Part 3 of the Cryptography Series! I highly recommend reading Part 2 before diving into this post. You can also explore the rest of the series here.
In this blog, we’ll dive deeper into semantic security, exploring examples and its implications. Alright, let’s get started!
Computing individual bits of a message
If a cryptosystem is secure, it should be difficult not only to recover the entire message but also to compute any partial information about it.
Here, we will not prove a fully general theorem, but instead, consider a specific example. Let $\mathcal{E} = (E, D)$ be an encryption scheme defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$, where $\mathcal{M} = \left\lbrace 0, 1\right\rbrace^L$. For a message $m \in \mathcal{M}$, we define $\mathsf{parity}(m)$ to be $1$ if the number of $1$s in $m$ is odd, and $0$ if it is even. In other words, $\mathsf{parity}(m)$ is the XOR sum of all the bits in $m$.
We will show that if $\mathcal{E}$ is semantically secure, then given the ciphertext $c$ of a random message $m$, it is difficult to predict $\mathsf{parity}(m)$. Since $\mathsf{parity}(m)$ is a single bit, any adversary can predict its value correctly with a probability of $1/2$ by random guessing. But what we want to show is that no efficient adversary can do significantly better than random guessing.
Using a similar proof method as in the Cryptography 2 post, let’s assume there is an efficient adversary $\mathcal{A}$ that can predict $\mathsf{parity}(m)$ with probability $1$. This means that for every message $m$, every key $k$, and every ciphertext $c$ of $m$, when we give $c$ to $\mathcal{A}$, it outputs the value $\mathsf{parity}(m)$. We can then use $\mathcal{A}$ to construct a semantic security ($\mathtt{SS}$) adversary $\mathcal{B}$ that works as follows: The adversary $\mathcal{B}$ chooses two messages $m_0$ and $m_1$ arbitrarily, but such that $\mathsf{parity}(m_0) = 0$ and $\mathsf{parity}(m_1) = 1$. It then sends these two messages to its challenger in its $\mathtt{SS}$ game, receives a ciphertext $c$, and forwards $c$ to $\mathcal{A}$. Upon receiving $c$, adversary $\mathcal{A}$ outputs a bit $\hat{b}$, and $\mathcal{B}$ outputs this same bit. It is easy to see that the $\mathtt{SS}$ advantage of $\mathcal{B}$ is exactly $1$: when the challenger encrypts $m_0$, $\mathcal{B}$ always outputs $0$, and when it encrypts $m_1$, $\mathcal{B}$ always outputs $1$. This leads to a contradiction because $\mathcal{E}$ is semantically secure. Therefore, if $\mathcal{E}$ is semantically secure, no efficient adversary can predict $\mathsf{parity}$ with probability $1$. However, we can say something stronger: if $\mathcal{E}$ is semantically secure, no efficient adversary can predict $\mathsf{parity}$ with a probability significantly greater than $1/2$. To state this precisely, we define an attack game:
The Parity Prediction Attack Game
For an encryption scheme $\mathcal{E} = (E, D)$ defined on $(\mathcal{K}, \mathcal{M}, \mathcal{C})$, and a given adversary $\mathcal{A}$, the attack game proceeds as follows:
- The challenger chooses $m \xleftarrow{R} \mathcal{M},\ k \xleftarrow{R} \mathcal{K},\ c \leftarrow E(k, m)$ and sends $c$ to the adversary.
- The adversary outputs a bit $\hat{b} \in \left\lbrace 0, 1\right\rbrace$.
Let $W$ be the event that $\hat{b} = \mathsf{parity}(m)$. We define the parity prediction advantage of $\mathcal{A}$ against $\mathcal{E}$ as:
$$ \mathtt{Parity}\text{adv}[\mathcal{A},\mathcal{E}] := \left| \Pr[W] - \frac{1}{2} \right|. $$
Definition (Parity Prediction Security)
An encryption scheme $\mathcal{E}$ is called secure against parity prediction if for every efficient adversary $\mathcal{A}$, the value $\mathtt{Parity}\text{adv}[\mathcal{A},\mathcal{E}]$ is negligible.
Theorem 1. Let $\mathcal{E} = (E, D)$ be an encryption scheme defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$ with $\mathcal{M} = \left\lbrace 0, 1\right\rbrace^L$. If $\mathcal{E}$ is semantically secure, then $\mathcal{E}$ is also secure against parity prediction.
Proof. Similar to the proof of Theorem 1 in the Cryptography 2 post, we prove by security reduction. Specifically, we will show that for every parity-predicting adversary $\mathcal{A}$ attacking $\mathcal{E}$ in the Parity Prediction Attack Game, there exists an $\mathtt{SS}$ adversary $\mathcal{B}$ attacking $\mathcal{E}$ in the Semantic Security Attack Game from Cryptography 2, where $\mathcal{B}$ is simply a “wrapper” around $\mathcal{A}$, such that:
$$ \mathtt{SS} \text{adv}[\mathcal{B},\mathcal{E}] = 2 \cdot \mathtt{Parity}\text{adv}[\mathcal{A},\mathcal{E}]. $$
Assume $\mathcal{A}$ is an adversary that can predict parity with probability $1/2 + \varepsilon$, i.e.:
$$ \mathtt{Parity}\text{adv}[\mathcal{A},\mathcal{E}] = |\varepsilon|. $$
Here is how we construct the $\mathtt{SS}$ adversary $\mathcal{B}$:
$\mathcal{B}$ generates a random message $m_0$, and sets $m_1 \leftarrow m_0 \oplus (0^{L-1} || 1)$, which means $m_1$ is identical to $m_0$ except for the last bit, which is flipped. Thus, $m_0$ and $m_1$ have opposite parities.
$\mathcal{B}$ sends the pair $(m_0, m_1)$ to its $\mathtt{SS}$ challenger, receives a ciphertext $c$ from the challenger, and forwards $c$ to $\mathcal{A}$.
When $\mathcal{A}$ outputs a bit $\hat{b}$, $\mathcal{B}$ will output $1$ if $\hat{b} = \mathsf{parity}(m_1)$, and $0$ otherwise. Correction from original text for a standard reduction: B should guess which message was encrypted. Let’s adjust slightly for clarity. B outputs 1 if $\hat{b} == \mathsf{parity}(m_1)$ and 0 if $\hat{b} == \mathsf{parity}(m_0)$ (assuming they are different). A more standard reduction is: B outputs 0 if $\hat{b} = \mathsf{parity}(m_0)$ and 1 if $\hat{b} = \mathsf{parity}(m_1)$. Let’s follow a clear reduction: When $\mathcal{A}$ outputs $\hat{b}$, $\mathcal{B}$ guesses that $m_0$ was encrypted if $\hat{b} = \mathsf{parity}(m_0)$, and that $m_1$ was encrypted if $\hat{b} = \mathsf{parity}(m_1)$. Let’s say $\mathcal{B}$ outputs $b’$ where $b’=0$ if $\hat{b} = \mathsf{parity}(m_0)$ and $b’=1$ otherwise.
Let $p_b$ be the probability that $\mathcal{B}$ outputs $1$ if the $\mathtt{SS}$ challenger encrypts $m_b$, for $b = 0, 1$. By definition:
$$ \mathtt{SS} \text{adv}[\mathcal{B},\mathcal{E}] = |p_1 - p_0|. $$
Let’s analyze the probabilities. The distribution of the challenge ciphertext $c$ given to $\mathcal{A}$ is identical to the distribution in the parity-prediction game. So, $\mathcal{A}$ outputs the correct parity with probability $1/2 + \varepsilon$.
- If the challenger encrypted $m_0$ (so the true bit is $b=0$), $\mathcal{A}$ outputs $\mathsf{parity}(m_0)$ with probability $1/2 + \varepsilon$. In this case, $\mathcal{B}$ outputs $0$. $\mathcal{A}$ outputs $\mathsf{parity}(m_1)$ with probability $1/2 - \varepsilon$. In this case, $\mathcal{B}$ outputs $1$. So, $p_0 = \Pr[\mathcal{B} \text{ outputs } 1 \mid b=0] = 1/2 - \varepsilon$.
- If the challenger encrypted $m_1$ (so the true bit is $b=1$), $\mathcal{A}$ outputs $\mathsf{parity}(m_1)$ with probability $1/2 + \varepsilon$. In this case, $\mathcal{B}$ outputs $1$. So, $p_1 = \Pr[\mathcal{B} \text{ outputs } 1 \mid b=1] = 1/2 + \varepsilon$.
Therefore:
$$ \mathtt{SS} \text{adv}[\mathcal{B},\mathcal{E}] = |p_1 - p_0| = |(1/2 + \varepsilon) - (1/2 - \varepsilon)| = |2\varepsilon| = 2 \cdot \mathtt{Parity}\text{adv}[\mathcal{A},\mathcal{E}], $$
which proves the theorem. □
Thus, we have shown that if an adversary can efficiently predict the parity of a message, then that adversary can be used to break semantic security. Conversely, if an adversary can break semantic security, then it can also efficiently predict some predicate of the message (the reader can attempt to prove the reverse direction as an exercise).
Consequences of Semantic Security
Next, we will examine the consequences of semantic security in the context of a specific example: an electronic betting game. The specific details of the example are not overly important, but this example illustrates how the assumption of semantic security is often used in practical applications.
Consider a highly simplified version of roulette, a game between a house and a player. The player gives the house $1. He can place one of two types of bets:
- “high or low”, or
- “even or odd”.
After the bet is placed, the house chooses a random number $r \in \left\lbrace 0, 1, \ldots, 36\right\rbrace$. The player wins if $r \ne 0$, and if:
- he bets “high” and $r > 18$,
- he bets “low” and $r \le 18$,
- he bets “even” and $r$ is even,
- he bets “odd” and $r$ is odd.
If the player wins, the house pays him 2 dollars (a net profit of 1 dollar); if he loses, the house pays nothing (a net loss of 1 dollar). Clearly, the house has a small but non-negligible advantage in this game: the probability of the player winning is $\frac{18}{37} \approx 48.65%$.
Now, suppose this game is played over the Internet. And suppose for technical reasons, the house publishes an encryption of $r$ before the player places a bet (perhaps so that a regulatory agency, which shares a key with the house, can decrypt it). The player is free to analyze this encryption before placing his bet — and of course, by doing so, the player might increase his probability of winning.
However, if the encryption scheme used is good enough, the player’s winning chances should not increase significantly. Let’s prove this, assuming that $r$ is encrypted using a semantically secure encryption scheme $\mathcal{E} = (E, D)$, defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$, where $\mathcal{M} = \left\lbrace 0, 1, \ldots, 36\right\rbrace$ (we will assume that all messages in $\mathcal{M}$ have the same length). From here on, we will call the player $\mathcal{A}$, to emphasize the “adversarial” nature of the player, and assume that $\mathcal{A}$’s strategy is modeled by an efficient algorithm.
The game is illustrated in Figure 1 below. Here, $bet$ represents one of the choices “high”, “low”, “even”, or “odd”. The player $\mathcal{A}$ sends $bet$ to the house, which then evaluates the function $W(r, bet)$, returning $1$ if the bet wins with $r$, and $0$ otherwise.
Define:
$$ \mathtt{IR}\text{adv}[\mathcal{A}] := \left| \Pr[W(r, bet) = 1] - \frac{18}{37} \right|. $$
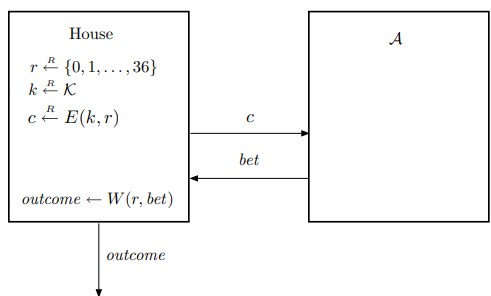Figure 1. Internet roulette
Our goal is to prove the following theorem:
Theorem 2. If $\mathcal{E}$ is a semantically secure encryption scheme, then for any efficient adversary $\mathcal{A}$, the value $\mathtt{IR}\text{adv}[\mathcal{A}]$ is negligible.
As in previous proofs, we will prove by reduction. More specifically, we will show that for each player $\mathcal{A}$, there exists an $\mathtt{SS}$ adversary $\mathcal{B}$, where $\mathcal{B}$ is a “simple wrapper” around $\mathcal{A}$, such that:
$$ \mathtt{IR}\text{adv}[\mathcal{A}] \le \mathtt{SS}\text{adv}[\mathcal{B}, \mathcal{E}]. \tag{1} $$
Thus, if there existed an efficient player $\mathcal{A}$ with a significant advantage, we would have an efficient $\mathtt{SS}$ adversary $\mathcal{B}$ that could break the semantic security of $\mathcal{E}$ — which we are assuming is impossible. This implies that no such $\mathcal{A}$ can exist.
To construct and analyze the adversary $\mathcal{B}$, we consider an idealized version of the Internet roulette game, where instead of publishing an encryption of the real value $r$, the house publishes an encryption of a dummy value, for example, $0$. The logic of this idealized game is illustrated in Figure 2. Note, however, that in the ideal game, the house still uses the real value $r$ to determine the outcome of the game.
Figure 2. Ideal Internet roulette
Let $p_{real}$ be the probability that player $\mathcal{A}$ wins in the real Internet roulette, and $p_{ideal}$ be the probability that $\mathcal{A}$ wins in the idealized version of roulette.
The adversary $\mathcal{B}$ is designed to participate in the Semantic Security Attack Game, such that we have:
- The real game corresponds to Experiment 0 (where $\mathcal{B}$ sends two messages, say $m_0=r$ and $m_1=0$, and receives an encryption of $m_0$).
- The ideal game corresponds to Experiment 1 (where $\mathcal{B}$ receives an encryption of $m_1$).
The logic of adversary $\mathcal{B}$ is illustrated in Figure 3. $\mathcal{B}$ runs $\mathcal{A}$ as a subroutine. In its own SS game, $\mathcal{B}$ chooses $m_0$ to be a random number $r \in \left\lbrace 0, \dots, 36\right\rbrace$ and $m_1$ to be the number $0$. It sends $(m_0, m_1)$ to its challenger. It receives a ciphertext $c$ back, which is either $E(k, m_0)$ or $E(k, m_1)$. $\mathcal{B}$ then gives $c$ to $\mathcal{A}$. $\mathcal{A}$ outputs a bet. $\mathcal{B}$ then checks if this bet would have won against $m_0=r$. If it wins, $\mathcal{B}$ outputs 1; otherwise, it outputs 0.
Let $p_0 = \Pr[\mathcal{B} \text{ outputs } 1 \mid \text{challenge is } E(k, m_0)]$. This is exactly the winning probability in the real game, so $p_0 = p_{real}$. Let $p_1 = \Pr[\mathcal{B} \text{ outputs } 1 \mid \text{challenge is } E(k, m_1)]$. This is exactly the winning probability in the ideal game, so $p_1 = p_{ideal}$.
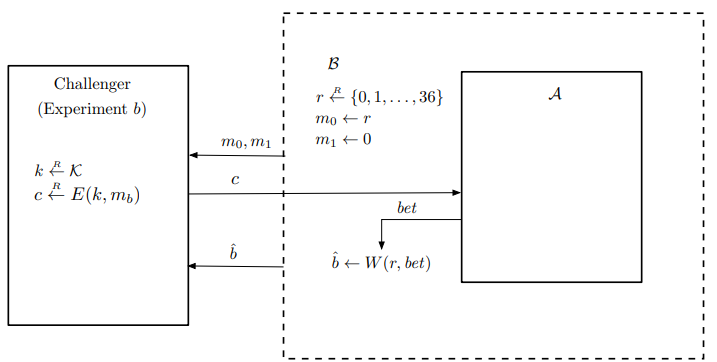Figure 3. The SS adversary B in the Semantic Security Attack Game
By the definition of semantic security advantage:
$$ \mathtt{SS}\text{adv}[\mathcal{B}, \mathcal{E}] = |p_1 - p_0| = |p_{ideal} - p_{real}|. \tag{2} $$
Now let’s consider the probability $p_{ideal}$ that $\mathcal{A}$ wins in the idealized version of roulette. No matter how clever $\mathcal{A}$’s strategy is, its winning probability is exactly $\frac{18}{37}$, because in the ideal version, the bet $bet$ is computed from the ciphertext $c$ — which is an encryption of the number $0$, and is therefore statistically independent of the value $r$. This means the ideal roulette is equivalent to real-life roulette where the player has no information. So, $p_{ideal} = \frac{18}{37}$.
By definition, $\mathtt{IR}\text{adv}[\mathcal{A}] = |p_{real} - \frac{18}{37}| = |p_{real} - p_{ideal}|$.
Combining this with (2), we get:
$$ \mathtt{IR}\text{adv}[\mathcal{A}] = |p_{real} - p_{ideal}| = \mathtt{SS}\text{adv}[\mathcal{B}, \mathcal{E}]. $$
This proves the desired relation. □
Conclusion
The method we used to analyze the Internet roulette game is an approach we will encounter many times in security analysis. The core idea is to replace a component in the system with an idealized version of that component, and then analyze the behavior of the new, idealized system. This is often called the real/ideal world paradigm.
Another lesson from the above example is that when reasoning about the security of a system, what we consider to be the “adversary” depends on the goal of the analysis. In the analysis above, we assembled a new adversary $\mathcal{B}$ from multiple components: part was the original adversary $\mathcal{A}$, and the rest was extracted from other components of the system (e.g., the house’s algorithm). This is very typical in security analyses.
Intuitively, if one imagines a system diagram, at different points in the analysis, one will draw a “circle” around different components to define “who the adversary is” at that moment.
Bit Guessing: An Alternative View of Semantic Security
The example above is a typical case of how one can use the definition of semantic security to analyze the security properties of a larger system that uses a semantically secure encryption scheme.
However, there is another interpretation of semantic security that is often more convenient when we want to prove that a specific encryption scheme satisfies this definition. In this alternative interpretation, we define a new attack game. The adversary’s role remains the same, but instead of having two different experiments, there is now only a single experiment.
In the bit-guessing version of the attack game, the challenger randomly chooses $b \in \left\lbrace 0, 1\right\rbrace$ and executes Experiment $b$ of the Semantic Security Attack Game. The adversary’s goal is to guess the bit $b$ correctly with a probability significantly better than 1/2.
The Semantic Security Attack Game (Bit-Guessing Version)
For an encryption scheme $\mathcal{E} = (E, D)$ defined over $(\mathcal{K}, \mathcal{M}, \mathcal{C})$, and a given adversary $\mathcal{A}$, the game proceeds as follows:
- The adversary chooses and sends two messages $m_0, m_1 \in \mathcal{M}$ of the same length to the challenger.
- The challenger randomly chooses $b \xleftarrow{R} \left\lbrace 0, 1\right\rbrace$, $k \xleftarrow{R} \mathcal{K}$, computes $c \leftarrow E(k, m_b)$, and sends $c$ to the adversary.
- The adversary outputs a bit $\hat{b} \in \left\lbrace 0, 1\right\rbrace$.
We say that the adversary wins the game if $\hat{b} = b$. □
Figure 4 illustrates the above Attack Game. Note that in this game, the event “adversary wins” is defined over the probability space induced by the random choice of $b$ and $k$, as well as any random choices made by the encryption algorithm and the adversary.
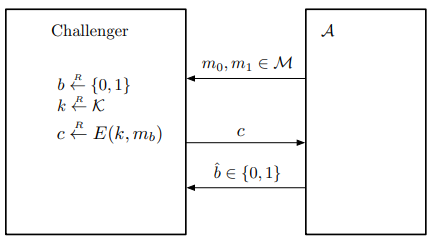Figure 4. The Semantic Security Attack Game (Bit-Guessing Version)
Of course, any adversary can win the game with probability $1/2$ by completely ignoring $c$ and guessing randomly (e.g., always guessing $\hat{b} = 0$ or always guessing $\hat{b} = 1$). What we are interested in is how much better than random guessing the adversary can do.
If $W$ is the event that the adversary wins the bit-guessing game, then the quantity we are interested in is $|\Pr[W] - 1/2|$, denoted by $\mathtt{SS}\text{adv}^*[\mathcal{A}, \mathcal{E}]$. We then have:
Theorem 3. For any encryption scheme $\mathcal{E}$ and any adversary $\mathcal{A}$, we have:
$$ \mathtt{SS}\text{adv}[\mathcal{A}, \mathcal{E}] = 2 \cdot \mathtt{SS}\text{adv}^*[\mathcal{A}, \mathcal{E}]. \tag{4} $$
Proof. This is a straightforward calculation. Let $p_0$ be the probability that the adversary outputs $1$ in Experiment 0 of the original Semantic Security Attack Game, and let $p_1$ be the probability that the adversary outputs $1$ in Experiment 1.
Now consider the bit-guessing version of the Semantic Security Attack Game. From here on, all events and probabilities are considered within this game.
If we condition on the event $b = 0$, then in this conditional probability space, all other random choices (of the challenger and the adversary) are distributed identically to those in Experiment 0. Therefore, if $\hat{b}$ is the adversary’s output in the bit-guessing game, we have:
$$ \Pr[\hat{b} = 1 \mid b = 0] = p_0. $$
Similarly:
$$ \Pr[\hat{b} = 1 \mid b = 1] = p_1. $$
Thus:
$$ \begin{aligned} \Pr[\hat{b} = b] &= \Pr[\hat{b} = b \land b = 0] + \Pr[\hat{b} = b \land b = 1] \\ &= \Pr[\hat{b} = b \mid b = 0] \cdot \Pr[b = 0] + \Pr[\hat{b} = b \mid b = 1] \cdot \Pr[b = 1] \\ &= \Pr[\hat{b} = 0 \mid b = 0] \cdot \frac{1}{2} + \Pr[\hat{b} = 1 \mid b = 1] \cdot \frac{1}{2} \\ &= \frac{1}{2} \left( (1 - \Pr[\hat{b} = 1 \mid b = 0]) + \Pr[\hat{b} = 1 \mid b = 1] \right) \\ &= \frac{1}{2} (1 - p_0 + p_1). \end{aligned} $$
Therefore:
$$ \mathtt{SS}\text{adv}^*[\mathcal{A}, \mathcal{E}] = \left| \Pr[\hat{b} = b] - \frac{1}{2} \right| = \left| \frac{1}{2} (1 - p_0 + p_1) - \frac{1}{2} \right| = \left| \frac{1}{2}(-p_0+p_1) \right| = \frac{1}{2} |p_1 - p_0| = \frac{1}{2} \cdot \mathtt{SS}\text{adv}[\mathcal{A}, \mathcal{E}]. $$
This proves the theorem. □
Just as we call $\mathtt{SS}\text{adv}[\mathcal{A}, \mathcal{E}]$ the “semantic security advantage” of $\mathcal{A}$, we will call $\mathtt{SS}\text{adv}^*[\mathcal{A}, \mathcal{E}]$ the “semantic-security bit-guessing advantage” of $\mathcal{A}$.
A Generalization
In fact, this situation is very general. Although we do not need it right now, for future reference, we will describe how to generalize this situation.
There will be many situations where a certain security property — let’s call it “$\mathtt{X}$” — for some cryptographic system — let’s call it “$\mathcal{S}$” — can be defined via an attack game consisting of two experiments, Experiment 0 and Experiment 1. In these, the adversary $\mathcal{A}$’s protocol is the same in both experiments, but the challenger’s protocol is different.
For $b = 0, 1$, we define $W_b$ as the event that the adversary outputs 1 in Experiment $b$, and define:
$$ \mathtt{X}\text{adv}[\mathcal{A}, \mathcal{S}] := \left| \Pr[W_0] - \Pr[W_1] \right| $$
as the X-advantage of adversary $A$ against system $S$.
Similar to the above, we can define a “bit-guessing” version of the attack game, where the challenger randomly chooses $b \in \left\lbrace 0, 1\right\rbrace$ and executes Experiment $b$. If $W$ is the event that the adversary’s output equals $b$, we define:
$$ \mathtt{X}\text{adv}^*[\mathcal{A}, \mathcal{S}] := \left| \Pr[W] - \frac{1}{2} \right| $$
as the X bit-guessing advantage of $\mathcal{A}$.
And with the exact same calculation as in the proof of Theorem 3, we obtain:
$$ \mathtt{X}\text{adv}[\mathcal{A}, \mathcal{S}] = 2 \cdot \mathtt{X}\text{adv}^*[\mathcal{A}, \mathcal{S}]. \tag{5} $$
Throughout this blog, we have delved into the rich and rigorous aspects of semantic security. There are three key lessons to take away:
Semantic security is a very strong guarantee. It means not only that an adversary cannot recover the entire message, but also that they cannot deduce any useful information about it. The example of being unable to predict the parity bit showed that the ciphertext is essentially a complete “black box” to the adversary.
Theory can be applied to analyze real-world systems. By using the technique of security reduction and the real/ideal world paradigm, we were able to draw a rigorous conclusion that a player cannot gain a significant advantage in the Internet roulette game if the house uses a semantically secure scheme. This is a core methodology in security analysis.
There are equivalent ways to view a security definition. The conversion from a distinguishing game to a bit-guessing game is not just an intellectual exercise. It provides a flexible and often easier-to-use tool for cryptographers when proving the security of new systems.
These concepts form the solid foundation upon which we will continue to build and analyze more secure encryption schemes in the upcoming articles of this series.
References
- Dan Boneh and Victor Shoup. A Graduate Course in Applied Cryptography. Retrieved from https://toc.cryptobook.us/
Connect with Me
Connect with me on Facebook, LinkedIn, via email at dangduongminhnhat2003@gmail.com, GitHub, or by phone at +84 829 258 815.