Posted on: August 6, 2024 | Reading time: 30 minutes | Word count: 6381 words | Author: Dang Duong Minh Nhat
In my research on security and privacy in ZK-EVM (Zero-Knowledge Ethereum Virtual Machine), it’s essential to understand the foundational concepts of Zero-Knowledge Proofs (ZKPs). ZKPs are a revolutionary cryptographic technique that enables one party to prove knowledge of a fact without revealing any information about the fact itself. This blog will delve into the classification of Zero-Knowledge Proofs, their various applications, and how they play a pivotal role in enhancing privacy and security in blockchain systems, particularly in the context of ZK-EVM.
Table of Contents
- Table of Contents
- Introduction to Zero Knowledge Proofs
- Proof Systems and Privacy
- Understanding Commitment Schemes and Their Applications
- Understanding Identification Schemes and Their Role in Security
- Classification and Applications of Zero Knowledge Proofs
- References
- Connect with Me
Introduction to Zero Knowledge Proofs
Introduction
In recent years, proof systems have garnered significant attention for their ability to verify the integrity of mathematical computations. For instance, they can be used to implement cryptographic checkers that certify whether a mathematical function, such as a search query on a database, has been computed correctly. This ensures the accuracy of the output even if the database is owned by a potentially dishonest party.
A standout feature of these proof systems is zero-knowledge, which ensures the privacy of the computational process. Zero-knowledge allows the verification of computations on a data set without revealing any specific information about the data itself. This makes zero-knowledge proof systems particularly valuable in privacy-sensitive areas such as anonymous identification, database membership queries, or blockchain-based payments.
Origins of Zero Knowledge
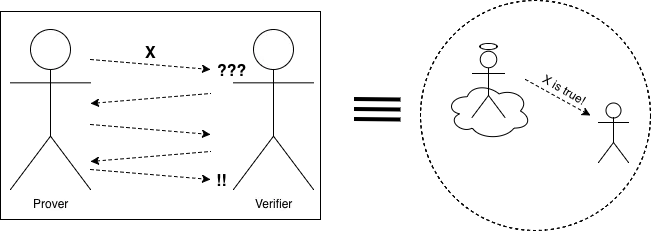
The concept of “zero knowledge” was first proposed in the 1980s by researchers Shafi Goldwasser, Silvio Micali, and Charles Rackoff of MIT in their paper “The Knowledge Complexity of Interactive Proof-Systems”. Their research focused on interactive proof systems, where one party (called the ‘Prover’) exchanges information with another party (the ‘Verifier’) to convince the Verifier that a certain mathematical statement is true. The goal of an interactive proof is to persuade the Verifier that a particular string belongs to a specific language. While the Prover is not limited in computational power, the Verifier is constrained.
Before the work of Goldwasser and colleagues, most research in this field emphasized the soundness of the proof system—ensuring that the Prover could not deceive the Verifier into believing a false statement. However, Goldwasser, Micali, and Rackoff posed a crucial question: what happens if the Verifier is not trustworthy?
They were concerned with information leakage and questioned how much additional information the Verifier could learn beyond just verifying the truth of a statement. This concern was not only theoretical but had significant practical implications.
For example, when a user logs into a web server using a password, the conventional method is to store a hashed version of the password on the server. The client sends the original password to the server, which then re-computes the hash and compares it to the stored value. The problem here is that the server knows the actual password, so if the server is compromised, the password is exposed.
Goldwasser, Micali, and Rackoff proposed zero-knowledge proofs as a solution to this problem. Zero-knowledge proofs allow us to prove statements without revealing any information other than the assertion that the statement is true. This concept opens new possibilities for protecting information in interactive proof systems, ensuring that sensitive information is not leaked during the verification process.
Proof Systems and Privacy
After introducing Zero Knowledge Proofs, let’s delve deeper into the concepts and mechanisms behind them. This section will explain what a proof system is, explore privacy concepts through Zero Knowledge Proofs, and cover the formal definitions necessary for a better understanding of these mechanisms. Let’s start by clarifying what a proof system is and why it is important.
What is a Proof System?
In computational complexity theory, an interactive proof system is an abstract machine that models the computational process as a message exchange between two parties. These parties, called the Prover and the Verifier, interact by exchanging messages to determine the truth of a statement.
The Prover is considered all-powerful, with unlimited computational resources, but cannot be fully trusted. On the other hand, the Verifier has limited computational power. Messages are exchanged between the Prover and the Verifier until the Verifier has enough evidence to either verify or reject a statement. All interactive proof systems possess two main properties:
Completeness: If the statement is true, an honest Verifier (one who follows the protocol correctly) can be convinced of the statement’s truth by an honest Prover.
Soundness: If the statement is false, no fraudulent or malicious Prover can convince an honest Verifier that the statement is true, except with negligible probability.
In other words, soundness ensures that the verification process cannot be “fooled” into accepting false statements. This represents the Verifier’s ability to protect itself from being persuaded by false claims (no matter how the Prover attempts to deceive). Completeness, on the other hand, simply represents the Prover’s ability to convince the Verifier of true statements (belonging to a set of predefined true statements). Both properties are essential to ensure the concept of a proof system.
Interactive proof systems are crucial for ensuring the integrity of computations, providing a way to verify the correctness of statements without revealing sensitive information.
Privacy through Zero Knowledge Proofs
Zero-knowledge proof systems have an additional remarkable property: they do not reveal any information beyond the validity of the statement. This property is meaningful only if the Prover possesses some secret information—known as a witness—and wants to ensure that the Verifier does not learn anything else about it. The third, and perhaps the most magical, property of zero-knowledge proof systems can be summarized as follows:
Zero-knowledge: If the statement is true, no dishonest Verifier can learn anything beyond the fact that the statement is true.
To illustrate this, let’s consider the following example: Suppose there is a cave with two paths connected by a door that can only be opened with a secret word. Alice wants to prove to Bob that she knows the secret word without revealing it. To do this, both stand at the entrance of the cave. Alice then walks into the cave and chooses one of the two paths at random. From the entrance, Bob cannot know which path Alice has taken.
Bob then enters the cave and arrives at the junction. He chooses one of the two paths and calls out to Alice to come through that path. Alice’s task is to appear on the path that Bob has chosen. If Alice happened to choose the same path that Bob called, she doesn’t need the secret word. But if she chose the other path, she must pass through the door to reach the correct path.
This means that if Alice does not know the secret word, she can only convince Bob that she knows the secret word with a 50% probability in a single execution of this protocol. Therefore, Alice and Bob will repeat the protocol many times to reduce the error probability to an insignificant level. This protocol is considered a zero-knowledge proof because, no matter how many times it is repeated, if Alice knows the secret word, she will always succeed in appearing on the correct path Bob calls for, while Bob learns nothing new about the secret word.
Zero-knowledge proof systems ensure that the verification process does not reveal any information other than the correctness of the statement, thereby protecting the privacy of the Prover’s secret information.
The Colored Balls and the Colorblind Friend: An Illustration of Zero Knowledge Proofs
To illustrate Zero Knowledge Proofs more clearly, let’s consider the following example:
Bob has a friend named Alice who is colorblind. Bob owns two balls: one red and one green, but they are identical in shape and size. To Alice, these two balls appear exactly the same, and she doubts they can be distinguished by color. Bob wants to prove to Alice that the two balls are indeed of different colors without revealing which one is red and which one is green.
To do this, Bob hands the two balls to Alice and asks her to switch them behind her back. After each switch, Bob will guess whether the two balls have been swapped.
The process goes as follows:
- Bob gives the two balls to Alice.
- Alice switches the two balls behind her back.
- Bob guesses whether Alice has swapped the balls or not.
If the two balls are of the same color, Bob can only guess correctly with a 50% probability. However, if they are of different colors, Bob can easily determine whether Alice has swapped the balls.
This process can be repeated multiple times. If Alice sees that Bob consistently guesses correctly, she will begin to believe that the two balls are indeed of different colors (completeness). If not, the probability that Bob could guess correctly all the times without any additional information will be nearly zero (soundness). Meanwhile, Alice still does not know which ball is red and which is green (zero knowledge).
Through this example, we see that a zero-knowledge proof system allows Bob to verify a statement without revealing any information about the nature of the two balls, thereby protecting the privacy of the secret information.
Formal Definitions
Interactive Turing Machines
While the properties of proof systems might seem intuitive, formally defining completeness, soundness, and zero-knowledge in a rigorous mathematical way has taken decades of research. To formalize these properties, we need a computational model to represent the interaction between two computing devices. In cryptography, the preferred choice is the Turing Machine, named after the “father” of computer science, Alan Turing.
Interactive Turing Machines
An Interactive Turing Machine (ITM) is a multi-tape (deterministic) version of the Turing Machine. The ITM consists of the following tapes:
- Input Tape: Read-only.
- Random Tape: Read-only.
- Work Tape: Read and write.
- Output Tape: Write-only.
- Communication Tapes: A pair of tapes, one read-only and one write-only.
- Switch Tape: Read and write, consisting of a single cell.
Each ITM is associated with a unique bit, called its identity. An ITM is said to be active when the content of the switch tape equals the machine’s identity. Otherwise, the machine is considered idle. When idle, the state of the machine, the position of the heads on the different tapes, and the content of the writable tapes do not change.
- Input: Content of the input tape.
- Random Input: Content of the random tape.
- Output: Content of the output tape at the end.
- Messages Sent: Content written on the write-only communication tape during the machine’s active period.
- Messages Received: Content read from the read-only communication tape during the machine’s active period.
The machine’s movement on both communication tapes is unidirectional, for example, from left to right.
Assume we call the interactive Turing machine M₁ the Prover $P$ and M₂ the Verifier $V$. Like humans, machines need to understand a language $L$ to interact correctly. We do not plan to delve deep into language and complexity theory here. All we need to know is that the statement the Prover $P$ wants to prove must be – loosely speaking – encoded in a specific language. With $(x, w) \in L$ and $(x, w) \notin L$, we denote a true or false statement to be proven. In other words, the pair $(x, w)$ is a member of the language $L$. Typically, the value $x$ is public and known to both the Prover and the Verifier, while the parameter $w$ (called the witness) is private and known only to the Prover.
Definition of Language $L$
Formally, a language $L$ is defined as a set (possibly infinite) of strings over some finite alphabet and is formed according to a set of specific rules. For example, a language $L$ over the alphabet $\sum = {0, 1, 2, -, =}$ may have the following grammar:
- Any non-empty string that does not contain “-” or “=” and does not start with “0” is in $L$.
- A string containing “=” is in $L$ if and only if it contains exactly one “=”, and it separates two valid strings of $L$.
According to these rules, the string “2–1=1” is in $L$, but the string “=21=0-” is not. During the setup phase of the communication protocol, the interacting parties usually agree on a specific language with specific rules.
By understanding these formal definitions, we gain a deeper insight into how interactive proof systems work, paving the way for robust zero-knowledge proofs that protect sensitive information while proving the validity of a statement.
Interactive Proof Systems: Understanding Their Mechanics
An interactive proof system is a critical component in the realm of cryptography, allowing a Prover $P$ to convince a Verifier $V$ of a statement’s validity without revealing any sensitive information. A pair of Interactive Turing Machines $(P, V)$ constitutes an interactive proof system for a language L if the Verifier operates in polynomial time and the following two conditions hold:
Completeness
The completeness property ensures that if the statement is true, the Prover can convince the Verifier with significant probability. Formally, for every pair $(x, w)$ in the language L, the probability that Prover $P$ can successfully convince the honest Verifier $V$ is expressed as:
$\forall (x, w) \in L: Pr[\langle P(x, w), V(x)\rangle = 1] \geq 1-negl$
This means that if $(x, w)$ is a valid statement in $L$, the Prover has a high chance of successfully convincing the Verifier.
Soundness
Soundness has two versions that together ensure the reliability of the proof system:
- Weak Soundness (Unforgeability): For any $(x, w)$ not in the language $L$, the probability that a dishonest Prover $𝑃^{’}$ can convince the honest Verifier $V$ is negligible:
$\forall (x, w) \notin L: Pr[\langle P^{’}(x), V(x)\rangle = 1] \leq negl$
This means that if $(x, w)$ is not a valid statement, it should be virtually impossible for a dishonest Prover to convince the Verifier.
- Strong Soundness (Special Soundness): For every $(x, w)$ in $L$, there exists a polynomial-time extractor algorithm $E$ such that the witness $w$ can be extracted from valid conversations between Prover $P$ and Verifier $V$:
$\forall (x, w) \in L, \exists E: Pr[E\langle P(x, w), V(x)\rangle = w] \geq 1-negl$
The strong soundness guarantees that the witness can be reliably extracted from the interaction, ensuring that the Prover’s knowledge can be verified.
These two versions of soundness emphasize that a valid proof should not only be convincing but also verifiable in a way that guarantees the integrity of the information.
Zero-Knowledge
The zero-knowledge property is perhaps the most fascinating aspect of interactive proof systems. For every $(x, w)$ in the language $L$, there exists a simulator $S$ such that no polynomial-time distinguisher $D$ can distinguish between the real interaction between Prover $P$ and Verifier $V$ and the simulated interaction produced by $S$:
$\forall (x, w) \in L, \forall V \exists S: Pr[D\langle P(x, w), V(x)\rangle = 1] - Pr[D\langle S(x)\rangle = 1] \leq negl$
This means that the interaction between the Prover and Verifier does not leak any information beyond the validity of the statement itself.
Understanding the Simulation Mechanism To grasp the simulation mechanism, it is essential to remember the concept of indistinguishability. Indistinguishability is a powerful notion in computer science that indicates when two distributions (or processes) cannot be distinguished from one another by a given algorithm $D$. If a spectator cannot differentiate between a human and a machine after a lengthy conversation, the machine is considered to be “as good as” or “appearing like” a human.
In the comparison between the interaction of Prover $P$ and Verifier $V$ with the execution process created by simulator $S, P$ uses her witness $w$ while simulator $S$ only has access to the public information $x$. Despite the information disadvantage, the simulator generates a “similar” record of the interaction between Prover and Verifier. If the actual protocol record is indistinguishable from the simulated record, then the protocol is considered zero-knowledge because the simulated record contains no information about the witness $w$.
Understanding Commitment Schemes and Their Applications
In the previous sections, we explored proof systems, the concept of privacy through Zero Knowledge Proofs, and some formal definitions. Now, we will delve into the intriguing world of Commitment Schemes and their applications, particularly in the context of graph coloring problems. Let’s start by understanding what a Commitment Scheme is, followed by its specific applications.
What is a Commitment Scheme?
A Commitment Scheme is a cryptographic method that allows one party (the sender) to commit to a value or message while keeping that value secret until the sender chooses to reveal it later. Commitment Schemes have two primary properties:
- Hiding Property: The receiver cannot determine the value that the sender has committed to until the sender reveals it.
- Binding Property: The sender cannot change the committed value after the commitment is made.
Visualizing the Concept
Imagine the sender places a message inside a locked box and hands the box to the receiver. The receiver cannot open the box and therefore cannot see the message inside. The sender holds the key and can choose to reveal the message by providing the key to the receiver later. In this analogy, the locked box represents the “commitment,” while the key symbolizes the “proof.”
Two Phases of a Commitment Scheme
Commitment Schemes consist of two main phases:
- Commit Phase: The sender selects and commits to a value.
- Reveal Phase: The sender reveals the committed value, and the receiver verifies its authenticity.
In our analogy, the commit phase occurs when the sender places the message in the box and locks it. The reveal phase takes place when the sender gives the key to the receiver to open the box and confirm the message inside.
Technical Characteristics
- Commit Phase:
- The sender produces a unique message known as the “commitment” to send to the receiver.
- This commitment must be designed so that the receiver cannot extract the committed value immediately (hiding property).
- Reveal Phase:
- The sender sends a unique message called the “opening” to the receiver.
- The receiver checks this message to verify the committed value (binding property).
Historical Development
- The concept of a Commitment Scheme was first formalized by Gilles Brassard, David Chaum, and Claude Crépeau in 1988, in the context of zero-knowledge protocols for NP problems.
- Before this formalization, several researchers, including Manuel Blum, Shimon Even, and Adi Shamir, had used the concept but had not formally defined it.
- The term “commitment” is believed to have originated from Manuel Blum.
Applications of Commitment Schemes
Commitment Schemes have numerous applications in cryptographic protocols, including:
- Secure Coin Flipping: Ensuring that neither party can manipulate the outcome of a coin flip.
- Zero-Knowledge Proofs: Proving that one party knows a value without revealing the value itself.
- Secure Computation: Ensuring that parties can perform computations on data without revealing the data to each other.
Commitment Schemes play a vital role in ensuring safety and security across various cryptographic protocols and applications.
Graph Coloring: A Dive into Zero-Knowledge Proofs
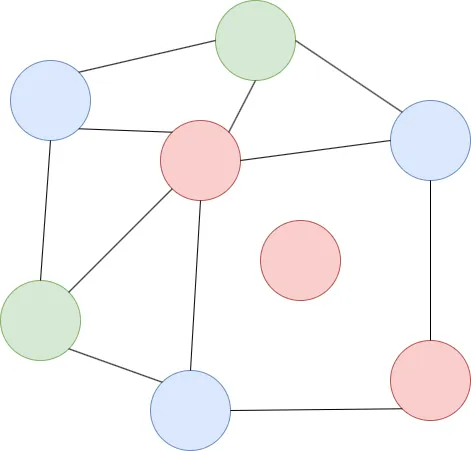
In the realm of cryptography, the problem of graph coloring offers an interesting application of Commitment Schemes and Zero-Knowledge Proofs (ZKPs). The objective in this scenario is for the prover to demonstrate that they have a valid coloring for a graph without revealing the entire coloring to the verifier. Let’s explore how this works, including the properties of Commitment Schemes, the interaction process, and the implications of Zero-Knowledge Proofs.
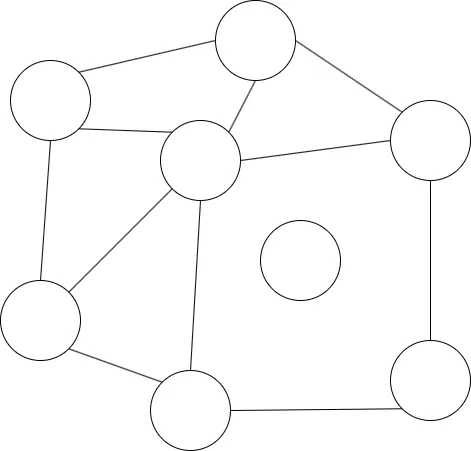
 Source Image
Source Image
Understanding the Graph Coloring Problem
Graph coloring is a classic problem in computer science where the goal is to assign colors to the vertices of a graph such that no two adjacent vertices share the same color. In our context, the prover wants to convince the verifier that they can color the graph correctly without disclosing the actual coloring method used.
Key Properties of Commitment Schemes
Commitment Schemes are essential to maintaining privacy and integrity in the graph coloring process. They possess two fundamental properties:
- Hiding: The verifier cannot discern the value the prover has committed to until it is revealed.
- Perfect Hiding: Even if the verifier has unlimited computational power, they cannot uncover the committed value.
- Binding: The prover cannot alter the committed value once it has been established.
- Perfect Binding: Again, even with unlimited computational resources, the prover cannot change their commitment.
In practice, achieving both perfect hiding and perfect binding simultaneously is impossible. Instead, we rely on computationally hiding and binding, which ensures these properties hold within the limits of computational capability.
Steps of Interaction Between Prover and Verifier
The interaction process in the graph coloring scenario unfolds through several key phases:
- Commit Phase: The prover commits to a coloring method and sends it to the verifier.
- Verifier Chooses: The verifier randomly selects two adjacent vertices to check and sends these vertices to the prover.
- Reveal Phase: The prover sends the keys of the commitment scheme corresponding to the chosen vertices.
- Verification: The verifier uses these keys to validate the colors of the two vertices.
- Repetition: This process is repeated multiple times, with the prover alternating colors each time to ensure that the colors revealed are from an independent random distribution.
What Makes a Proof Zero-Knowledge?
A proof is considered truly zero-knowledge if, at the end of the interaction, the verifier gains no additional information about the secret, despite having participated in the protocol. Essentially, the verifier should not learn anything extra by observing the messages exchanged between the prover and themselves. These messages are referred to as the transcript.
Due to the randomness utilized in ZKPs—such as the random selection of revealed vertices in the graph coloring problem—numerous transcripts can be generated from a foundational probability distribution. A simulator, designed as a third-party algorithm, generates transcripts from the same distribution. The objective is to ensure that the messages produced during the proof and the outputs from the simulator are indistinguishable.
The key point here is that if we can construct a simulator that operates without accessing the prover’s secret, it guarantees that the verifier does not learn any information from the communication process. The simulator must produce transcripts that the verifier cannot distinguish from those created during the actual proof. If this can be achieved without knowing the prover’s secret, we can confirm that the protocol is indeed zero-knowledge.
A proof is considered perfect zero-knowledge if, for all possible verifiers, there exists a simulator with access to that verifier such that the distributions of actual transcripts and the simulator’s outputs are identical. This implies that at the end of the proof, the verifier learns nothing additional about the prover’s secret, even though they participated in the protocol.
In practice, weaker definitions of zero-knowledge are often used:
- Statistical Zero-Knowledge: Requires the distributions to be statistically close, meaning that an unlimited computational program, with a polynomially bounded number of samples, cannot distinguish between the two distributions.
- Computational Zero-Knowledge: An even weaker variant where a computationally bounded program (with polynomial time limits) cannot differentiate between the two distributions with a limited number of samples.
Designing a Simulator for ZKP in Graph Coloring
To design a simulator that can access any verifier and generate transcripts for ZKP in the Three Coloring problem, we need to follow these steps:
- Randomly select a pair of adjacent vertices and color them differently.
- Randomly assign colors to the remaining vertices.
- Execute an arbitrary verifier (with access to the committed colors) to obtain a selected pair of adjacent vertices. If the chosen pair does not match those colored differently in step 1, repeat the process.
- Present (A) the corresponding commitment for the assigned colors, (B) the selected vertices, and (C) the corresponding keys.
To ensure the simulator does not run indefinitely, we can impose a limit on the number of restarts. If the limit is exceeded, the simulation “fails” but still meets the definition of a simulator.
When considering the distributions of the simulator’s output vertices and the interaction between a valid prover and any verifier, it becomes clear that they are equivalent. We can simply observe the similarities between the commitments and keys of the actual transcript and the simulated transcript.
The Complexity of the Three Coloring Problem
It’s crucial to note that a commitment scheme cannot satisfy both perfect hiding and perfect binding. In fact, it is also impossible to achieve both statistically. At least one of these properties must hold computationally.
To ensure perfect hiding, at least two distinct messages must produce the same commitment output. This leads to commitments that can be satisfied by more than one input, making it impossible to guarantee perfect binding.
The Three Coloring problem is a significant challenge in computer science and is classified as NP-Complete. This means that all problems that can be efficiently computed or verified can be simulated by a Three Coloring solution. ZKPs for the Three Coloring problem demonstrate that all problems within the NP class, including the most critical issues in computer science, can be proven within zero knowledge.
Understanding Identification Schemes and Their Role in Security
In the previous section, we explored the concepts of Commitment Schemes and their application in the graph coloring problem. In this section, we will delve deeper into identification schemes, particularly Schnorr’s Identification Scheme. These schemes play a crucial role in protecting personal information and ensuring safety in online transactions.
The Importance of Zero-Knowledge Proofs
Zero-Knowledge Proofs (ZKPs) allow for authentication schemes to defend against various attacks such as eavesdropping, social engineering, keylogging, and data breaches. Schnorr’s Identification Scheme is one such algorithm that leverages ZKPs to enhance security without compromising user privacy.
Traditional authentication schemes rely on users confirming their identity by sharing a secret, such as a password or PIN. However, a more effective solution enables users to prove their identity to a verifier without revealing any information that an eavesdropper or the verifier might find “interesting.” This approach minimizes the risk of exposing sensitive data while still verifying the user’s identity.
Introducing Schnorr’s Identification Scheme
Schnorr’s Identification Scheme, developed by Claus-Peter Schnorr in the 1980s, may initially appear unconventional, but it forms the foundation of many modern signature schemes. Interestingly, Schnorr’s primary focus was on identification rather than digital signatures.
To fully appreciate Schnorr’s Identification Scheme, let’s first cover some foundational concepts in group theory and how they relate to this identification process.
Background: Group Theory Essentials
Group Definition
A group is a non-empty set equipped with a binary operation (such as addition or multiplication) that satisfies the following conditions:
- Associativity: The operation is associative; for all elements $a,b,c$ in the group, $(a \cdot b) \cdot c = a \cdot (b \cdot c)$.
- Identity Element: There exists an identity element $e$ such that for every element $a$ in the group, $e \cdot a = a \cdot e = a$.
- Inverse Element: Each element $𝑎$ in the group has an inverse element $𝑎^{-1}$ such that $$𝑎 ⋅ 𝑎^{−1} = 𝑎^{−1} ⋅ 𝑎 = 𝑒$$
- Closure: For any elements $a$ and $b$ in the group, the result of the operation $a \cdot b$ is also in the group.
Cyclic Groups
A group is cyclic if it can be generated by a single element, known as a generator. This means every element in the group can be expressed as a power of that generator.
The Discrete Logarithm Problem
In cryptography, we often rely on functions that are easy to compute in one direction but hard to reverse. An example of this is the discrete logarithm.
Consider an element $h$ in $Z_p^*$ with a generator $g$ and an integer $𝑥$ such that $$𝑔^𝑥 \equiv ℎ \text{ mod } p$$Calculating $ℎ$ given $𝑥$ is relatively straightforward. However, for a suitably large prime $𝑝$, determining $𝑥$ given $ℎ$ becomes significantly more challenging. Since $𝑔$ is a primitive root, the probability of a random guess for $𝑥$ satisfying the equation is as low as $1 / 𝑝$.
While there are methods to improve the random approach, no known algorithms efficiently solve the discrete logarithm problem in general cases. This assumption underpins many algorithms in cryptography, including Schnorr’s Identification Scheme, where the prover authenticates their identity by demonstrating knowledge of the discrete logarithm without revealing the solution itself.
Schnorr’s Identification Scheme: A Deep Dive into Zero-Knowledge Proofs
Schnorr’s Identification Scheme is one of the cryptographic protocols that employs the concept of Zero-Knowledge Proof (ZKP). It allows a prover to convince a verifier that they know a secret value without actually revealing that value. In this post, we will explore the structure, properties, and functioning of this scheme.
Definition and Structure
To begin with, we define two large prime numbers, $𝑝$ and $𝑞$, such that $𝑞$ divides $𝑝 − 1$, $(𝑞 ∣ (𝑝 − 1))$. We then select $𝑔$ as a generator for a subgroup $𝐺$ (of prime order $𝑞$) of $Z_p^*$. A subgroup of a group is a subset of numbers that satisfies the properties of a group, and the order of a group is the number of elements in that group. This subgroup $G$ is known as the Schnorr Group. Finally, the private key $x$ (which identifies the prover) has a corresponding public key $X$ that satisfies the equation $$𝑋 = 𝑔^x \text{ mod } p$$
The Process of the Identification Scheme
The Schnorr Identification Scheme consists of the following steps:
- Commitment Step: The prover selects a random number $𝑣$ and sends a commitment $𝑉 = 𝑔^𝑣$ mod $𝑝$ to the verifier.
- Challenge Step: The verifier chooses a random number $𝑐$, known as the challenge, and sends it to the prover.
- Response Step: The prover calculates and returns the response $𝑏 = 𝑣 + 𝑐𝑥$ mod $𝑞$ to the verifier.
- Verification Step: The verifier checks if $$g^b = V \cdot X^c \text{ mod } p.$$
Sigma Protocols
The Schnorr Identification Scheme follows a three-step structure (commitment, challenge, response) and meets the properties of Zero-Knowledge (ZK) completeness, special soundness, and honest verification, collectively known as Sigma Protocols (or $\sum$-protocols). A replica of such protocols is often summarized as a tuple $(𝑉, 𝑐, 𝑏)$.
Completeness
The protocol is complete if a prover who knows 𝑥 can always convince an honest verifier. This is straightforward to see by confirming the verifier’s final check in step 4. Specifically, we have: $$g^b = g^v+cx=g^v \cdot g^{cx} = V \cdot X^c \text{ mod } p$$
Soundness
The protocol ensures that a dishonest prover, who does not know 𝑥, cannot convince the verifier with a high probability (reasonable error). This is proven by contradiction. If a dishonest prover can provide two responses $𝑏_1$ and $𝑏_2$ for the same commitment $𝑣$ but with two different challenges $𝑐_1$ and $𝑐_2$, we get: $$g^{b_1} = g^v \cdot g^{xc_1}$$ and $$g^{b_2} = g^v \cdot g^{xc_2}$$ From this, we can calculate $𝑥$ as: $$x = \frac{b_1 - b_2}{c_1 - c_2}$$ This contradicts the assumption that the prover does not know $𝑥$.
Proofs of Knowledge
A complete protocol is called a Proof of Knowledge (PoK) if it guarantees that the prover actually knows a secret value (like the private key $𝑥$) if they can convince the verifier. This means if the prover can persuade the verifier they know $𝑥$, then they must truly know it.
To demonstrate that the protocol is a Proof of Knowledge, we need to establish the existence of a special algorithm called an extractor. This extractor can obtain information from a potentially dishonest prover and compute the secret value $𝑥$.
Key Components
- Extractor: An assumed algorithm that has access to the prover and can derive the secret $𝑥$.
- Oracle Access: The extractor can perform operations or queries (imagine making phone calls) to gather necessary data from the prover.
- Adversarial Prover: This is a prover who does not necessarily follow the protocol honestly and may attempt to cheat or perform other actions.
- Probability of Convincing: If the prover can convince the verifier that they know $𝑥$ with a certain probability, the extractor can also compute $𝑥$ with at least that same probability.
For example, if a dishonest prover can generate proofs $(𝑉, 𝑐, 𝑏)$ that the verifier accepts with probability $P^{*}$, then the extractor can use these proofs to calculate $𝑥$ with probability at least $P^{*}$.
Special Soundness
The Sigma protocol guarantees that for any two accepted copies of the protocol $(𝑉, 𝑐, 𝑏)$ and $(𝑉, 𝑐^{’}, 𝑏^{’})$ where $𝑐$ and $𝑐^{’}$ are different, an efficient extractor can learn the witness $𝑥$. This validates that Schnorr’s Identification Scheme satisfies special soundness.
Honest-Verifier Zero-Knowledge (HVZK)
The final property we examine is Honest-Verifier Zero-Knowledge (HVZK). The goal here is to create a proof that the verifier cannot distinguish from the real proof, even when the verifier acts honestly.
We illustrate HVZK by constructing a simulator that can create fake proofs indistinguishable from real proofs. Here’s how the simulator works:
- Randomly Choose Response and Challenge: The simulator randomly selects a response value 𝑏 and a challenge value $𝑐$.
- Calculate Commitment Value: The simulator computes the commitment value $𝑉$ using the formula:
$$V = g^b \cdot X^{-c} \text{ mod } p$$
where:
- $g$ is the generator for the subgroup $𝐺$
- $𝑋$ is the public key $$𝑋 = g^x \text{ mod }p$$
- $𝑝$ is a large prime number
- Publish Proof: The simulator outputs a proof in the form $(𝑉, 𝑐, 𝑏)$.
Explanation
When the verifier selects random challenges, the proofs generated by the simulator are indistinguishable from real proofs created by an actual prover. This means that the verifier cannot determine whether the proof $(𝑉, 𝑐, 𝑏)$ was generated by the simulator or the real prover.
Example Illustration
Suppose the verifier receives a proof $(𝑉, 𝑐, 𝑏)$. If this proof cannot be distinguished from a real proof, it indicates that the verifier cannot ascertain how $(𝑉, 𝑐, 𝑏)$ was created, demonstrating the HVZK property.
Conclusion
Schnorr’s Identification Scheme offers numerous advantages over traditional authentication protocols (which rely on passwords). It ensures the security of the prover, even if the server (verifier) is compromised. However, its primary drawback is its single point of failure: the private key. Nonetheless, Schnorr’s scheme remains a potential solution to enhance the security toolkit for engineers.
Classification and Applications of Zero Knowledge Proofs
Zero Knowledge Proofs (ZKPs) are powerful cryptographic protocols that allow one party (the prover) to convince another party (the verifier) that a statement is true without revealing any additional information. In this post, we will classify ZKPs into two main types and explore their various applications.
Classification of Zero Knowledge Proofs
Interactive Zero Knowledge Proofs (IZKPs)
Interactive Zero Knowledge Proofs require multiple interactions between the prover and the verifier. This method allows the prover to convince the verifier of the validity of a statement without disclosing any other information. Here are the key features:
- Continuous Interaction: The prover and verifier must exchange multiple messages back and forth.
- Real-World Applications: While IZKPs can be used in various situations, they are not suitable for blockchain applications. Each interaction incurs gas fees, which can hinder the scalability of the system.
Non-Interactive Zero Knowledge Proofs (NIZKPs)
Non-Interactive Zero Knowledge Proofs only require a single interaction between the prover and the verifier. This characteristic makes them easier to implement on blockchain and other distributed systems. Key points include:
- Single Interaction: The prover prepares a single proof and sends it to the verifier. The verifier then checks the validity of the proof without any further interaction.
- Simulation Method: The prover simulates the necessary interactions and sends the results of this simulation to the verifier. The verifier checks and confirms that the simulation is accurate.
- Complex Cryptography: NIZKPs use sophisticated cryptographic techniques, though we won’t delve into these details in this report.
- Popular Types: Two of the most common NIZKPs are Zero Knowledge Succinct Non-interactive Argument of Knowledge (ZK-SNARKs) and Zero Knowledge Scalable Transparent Argument of Knowledge (ZK-STARKs).
Applications of Zero Knowledge Proofs
Zero Knowledge Proofs have a wide range of applications, some of which include:
- Privacy in Blockchain: While the transparency of blockchain offers advantages, such as the ability to verify public transactions, it can also lead to reduced privacy. ZKPs can protect transactions on the blockchain, enabling private transactions, secure messaging, and more. Examples of privacy-focused blockchains or protocols include Zcash, Mina, and Monero.
- Scalability of Blockchain: Ethereum’s Proof of Work model enhances the security of decentralized protocols but is resource-intensive and requires significant computational power to operate. With the advent of zk-rollups, we can bundle hundreds or thousands of transactions into a single proof for verification. This approach improves scalability by allowing these transactions to be recorded on Ethereum simultaneously, rather than processing each one directly on the blockchain.
- Authentication: ZKPs are widely used in authentication protocols as they provide a means to verify users without requiring private information like passwords or IDs. This enhances security while protecting user privacy.
- Machine Learning: ZKPs are also being applied in the field of machine learning. They allow algorithm owners to convince others of the outcomes of their models without disclosing any information about the actual machine learning model itself.
References
- Matthew Green. (2014, November 27). Zero Knowledge Proofs: An illustrated primer. Retrieved from https://blog.cryptographyengineering.com/2014/11/27/zero-knowledge-proofs-illustrated-primer/
- Yannik Goldgräbe, Sebastian Gajek. (2019, January 15). On Interactive Proofs and Zero-Knowledge: A Primer. Retrieved from https://medium.com/magicofc/interactive-proofs-and-zero-knowledge-b32f6c8d66c3
- Darlington Nnam. (2022, August 20). Beginner’s Guide To Understanding Zero Knowledge Proofs. Retrieved from https://medium.com/@darlingtonnnam/beginners-guide-to-understanding-zero-knowledge-proofs-cadc4e2c23a8
- Commitment scheme. Wikipedia. Retrieved from https://en.wikipedia.org/wiki/Commitment_scheme
- Noah. (2023, July 13). Zero-Knowledge Proofs. Retrieved from https://medium.com/@noah_h/zero-knowledge-proofs-3f412d911b1e
- Matthew Green. (2017, January 21). Zero Knowledge Proofs: An illustrated primer, Part 2. Retrieved from https://blog.cryptographyengineering.com/2017/01/21/zero-knowledge-proofs-an-illustrated-primer-part-2/
- Noah. (2023, August 19). Schnorr’s Identification Scheme. Retrieved from https://medium.com/@noah_h/schnorrs-identification-scheme-e9c029500cbd
Connect with Me
Connect with me on Facebook, LinkedIn, via email at dangduongminhnhat2003@gmail.com, GitHub, or by phone at +84829258815.