Posted on: August 15, 2024 | Reading time: 10 minutes | Word count: 2063 words | Author: Dang Duong Minh Nhat
Building on the foundations laid in our previous blog, we now take a deeper dive into the practical applications of these concepts. In this post, we’ll explore how arithmetic circuits play a pivotal role in zero-knowledge proofs, using the familiar game of Sudoku to demystify these complex ideas. Whether you’re expanding your cryptographic knowledge or new to the field, this blog will guide you through the intricacies of verifying solutions without revealing them, highlighting the profound impact on privacy and security in the digital age.
Table of Contents
- Table of Contents
- Exploring Binary Circuits: The Foundation of Digital Technology
- Unveiling Arithmetic Circuits: The Power Behind Efficient Polynomial Computation
- Unlocking the Secrets of Zero-Knowledge Proofs: The Role of Arithmetic Circuits
- References
- Connect with Me
Exploring Binary Circuits: The Foundation of Digital Technology
In the world of computing, everything starts with the bit – the smallest unit of data. A bit, represented as either 0 or 1, is the fundamental building block of all digital operations. But how do binary circuits work, and what role do they play in computers? Let’s dive into this fascinating world.
Logic Gates and Operations: The Heart of Binary Circuits
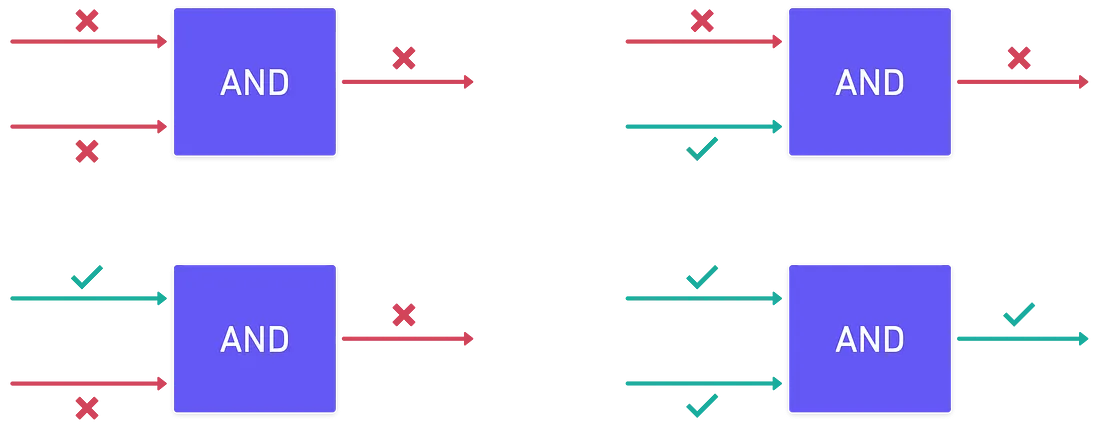
At the core of a binary circuit are logic gates, tiny electronic switches that process bits to perform basic operations. Imagine trying to solve a simple problem: if two conditions are true, you want the result to be true; otherwise, it’s false. This is precisely what an AND gate does – it only outputs a 1 when both inputs are 1; otherwise, it outputs a 0.
Beyond the AND gate, there are several other types of gates like NOT, OR, XOR, NAND, NOR, and XNOR, each serving a specific function depending on how the circuits are arranged. For instance, a NOT gate flips a bit – turning 1 into 0 and vice versa; an OR gate outputs 1 if at least one input is 1; while an XOR gate outputs 1 only when the inputs are different.
Circuit Layouts: Connecting the Dots
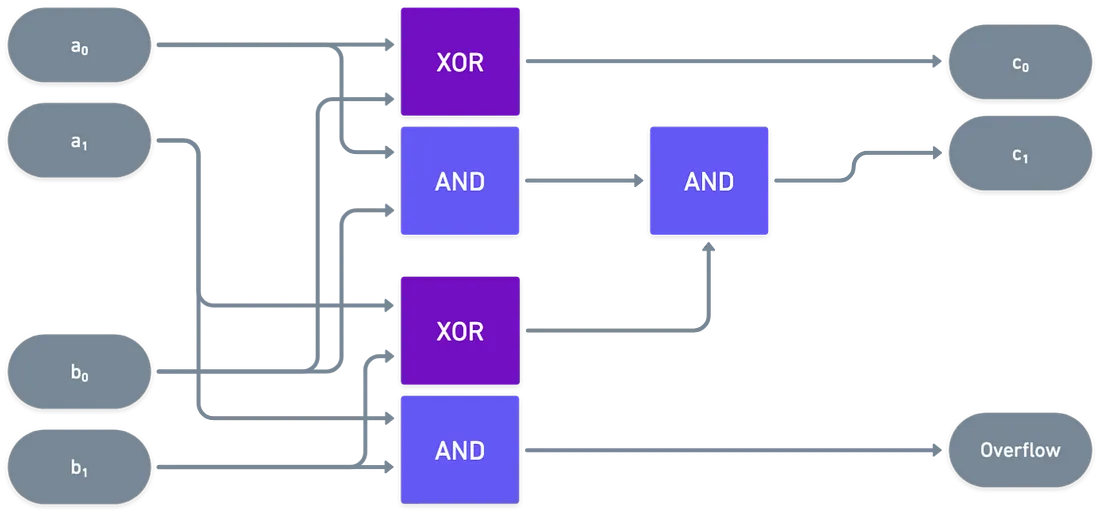
By linking multiple logic gates together, we create a circuit. This is where things get really interesting. Circuits allow us to perform more complex operations involving multiple inputs and outputs. For example, when adding two two-bit numbers, the circuit must handle not just the inputs but also the possibility of overflow – when the sum exceeds the capacity of the output bits.
Imagine adding two two-bit numbers: $A = \left(a_0,a_1\right)$ and $B = \left(b_0,b_1\right)$. While this might seem straightforward, to ensure accuracy, the circuit must consider all possibilities, including cases where the sum exceeds the bit capacity. This is where circuit design becomes crucial, enabling efficient and accurate calculations.
A Mathematical Perspective: Bits as Elements of a Finite Field
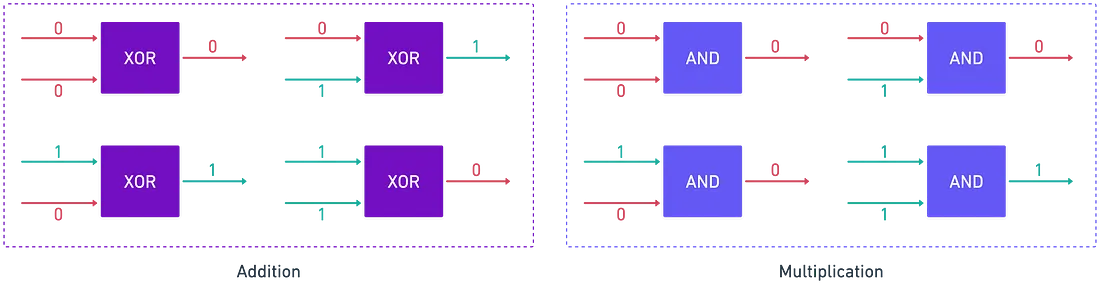
From a mathematical standpoint, a bit can be viewed as an element of the finite field {0,1}. Within this field, we can perform basic arithmetic operations like addition, multiplication, subtraction, and division (except by zero). The key is that all operations are performed under modulo 2, meaning the results are always either 0 or 1.
For example, adding 1 + 1 in modulo 2 results in 0. This concept also extends to how logic gates operate from a mathematical perspective. An XOR gate, for instance, performs addition modulo 2, while an AND gate performs multiplication modulo 2.
Polynomial Representation: From Logic Gates to Polynomials
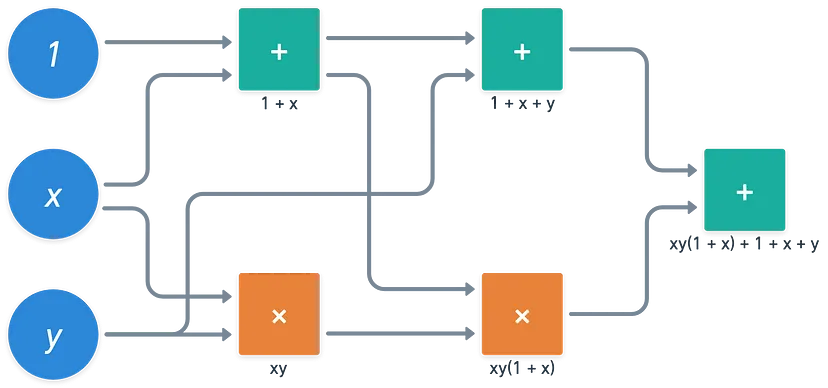
Now, here’s the exciting part. If we treat the inputs to a circuit as variables (like $x$ and $y$) and add a constant input of 1, the outputs from the logic gates can be expressed as a polynomial. This polynomial effectively captures the entire operation of the circuit in mathematical terms.
Polynomials aren’t just abstract concepts – they have practical applications in fields like cryptography. But why stop at operations under modulo 2? By extending this idea to other finite fields, we could unlock new possibilities for applying these concepts in various computational and cryptographic contexts.
Unveiling Arithmetic Circuits: The Power Behind Efficient Polynomial Computation
In the realm of computing and cryptography, the concept of Arithmetic Circuits plays a crucial role in efficiently performing complex polynomial computations, especially within the context of finite fields. But what exactly are arithmetic circuits, and why are they so vital? Let’s explore.
Understanding Arithmetic Circuits
At its core, an arithmetic circuit is a structured way to compute polynomial expressions, much like how binary circuits handle bits. However, the key difference lies in the field of operation. Instead of performing operations modulo 2 (as in binary circuits), arithmetic circuits operate within a finite field with $q$ elements—essentially performing operations modulo $q$.
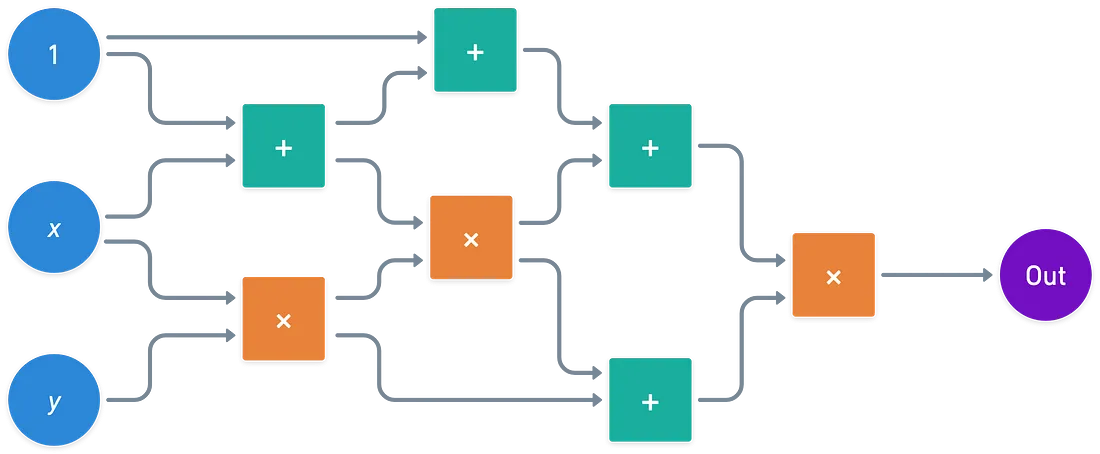
Imagine you have a polynomial like $x^4y^2+3x^3y^2+x^3y+2x^2y^2+4x^2y+4xy$. An arithmetic circuit would take this polynomial and break it down into smaller, manageable operations. These operations are then performed by nodes (or gates) in a directed acyclic graph (DAG), ensuring that the computation flows in one direction without looping back on itself.
Why Arithmetic Circuits?
One might wonder why we bother with such a complex structure when we could directly compute the polynomial if we know the formula and coefficients. The answer lies in the unique advantages offered by arithmetic circuits:
- Decomposability: Breaking down a polynomial into simpler steps allows us to better understand and manipulate the computation process. This is particularly useful in cryptographic protocols where clarity and control over each operation are essential.
- Parallelizability: Arithmetic circuits are designed in a way that allows independent operations to be executed simultaneously. This means that the circuit can handle multiple parts of a polynomial at the same time, significantly improving efficiency—an important consideration in resource-constrained environments like blockchain technology.
- Generality: The circuit-based approach is highly adaptable. It can accommodate a wide range of operations while preserving the algebraic properties of the polynomial. This generality is especially beneficial in homomorphic encryption, where computations are performed on encrypted data without decrypting it first. By maintaining the algebraic structure, arithmetic circuits ensure that these operations are accurate and secure.
Efficiency and Resource Considerations
The beauty of arithmetic circuits lies in their computational efficiency. The operations of addition and multiplication within these circuits are relatively inexpensive in terms of computational resources. This efficiency makes arithmetic circuits particularly well-suited for environments where processing power or memory is limited.
Moreover, the structure of an arithmetic circuit as a DAG ensures that computation is both straightforward and reliable. Since the circuit is acyclic, there’s no risk of running into circular dependencies or infinite loops—every operation moves forward, leading to a single, definitive result.
The Bigger Picture: Arithmetic Circuits in Cryptography
The use of arithmetic circuits goes beyond just polynomial computations—they are a cornerstone in modern cryptographic protocols. For example, in homomorphic encryption, where the goal is to perform operations on encrypted data without needing to decrypt it, arithmetic circuits allow for complex computations to be carried out while preserving the integrity of the data.
By breaking down complex polynomials into basic operations, arithmetic circuits make it possible to efficiently and securely compute on data in ways that would be impractical with traditional methods.
Unlocking the Secrets of Zero-Knowledge Proofs: The Role of Arithmetic Circuits
In the world of cryptography, where security and efficiency are paramount, zero-knowledge proofs stand out as a remarkable concept. They allow one party (the prover) to convince another party (the verifier) that they know a solution to a problem without revealing the solution itself. But how is this even possible? The answer lies in the clever use of arithmetic circuits. Let’s dive into how these circuits play a crucial role, with a familiar example—Sudoku—to guide us.
Sudoku as a Verification Problem
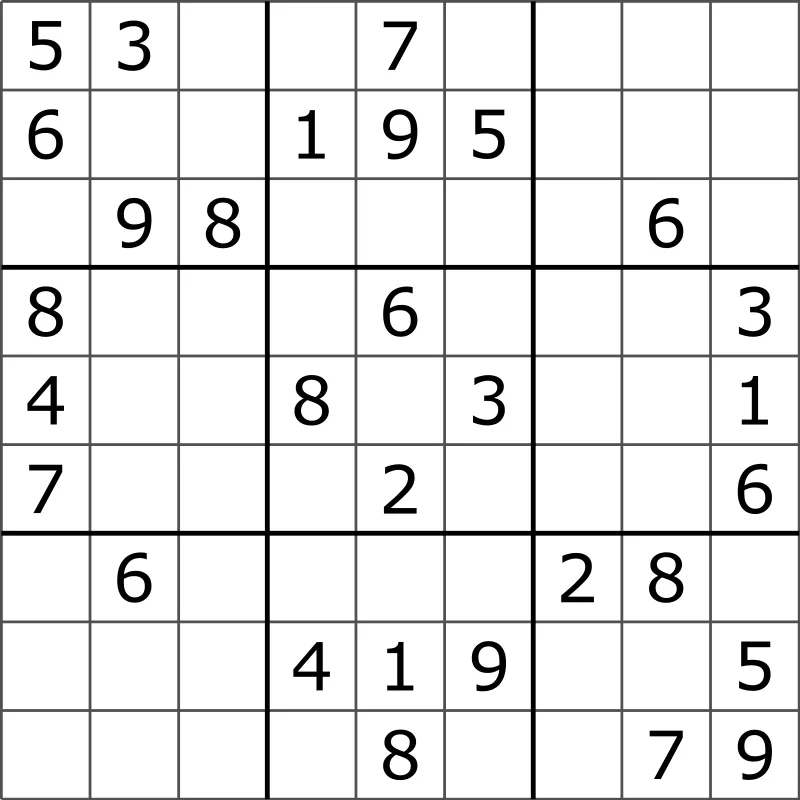
Sudoku, the classic 9×9 puzzle, offers more than just a fun challenge. It also provides an excellent analogy for understanding how zero-knowledge proofs work. The goal in Sudoku is simple: fill the grid so that each row, column, and 3×3 subgrid contains the numbers 1 through 9, with no repetitions. While solving Sudoku puzzles can be tricky, verifying a completed solution is straightforward—just check for duplicates.
This distinction between solving and verifying is not just a quirk of Sudoku; it’s a fundamental principle in computational theory. Many problems are difficult to solve but easy to verify once a solution is presented. This principle is at the heart of the famous P vs NP problem in computer science, a puzzle that has stumped the brightest minds and carries a one-million-dollar reward for a solution.
Verification Process in Sudoku
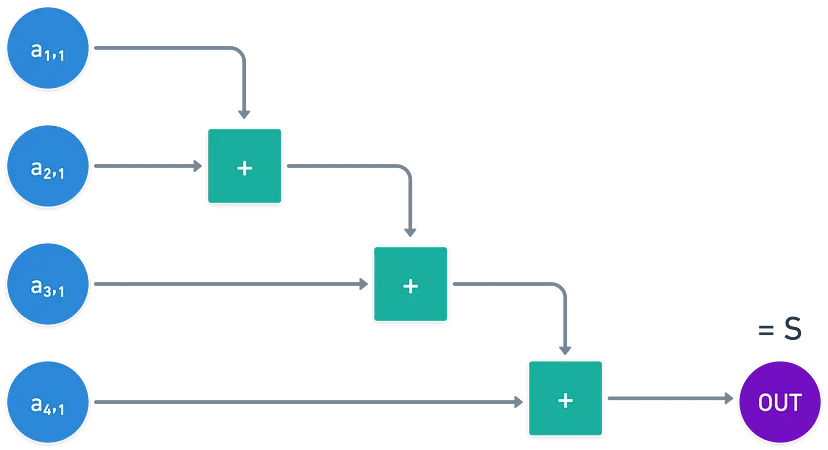
To put this in mathematical terms, verifying a Sudoku solution can be expressed through simple equations. Consider the grid as a matrix. For each row, column, and subgrid, the sum of the numbers must equal a specific value, say $S$, which represents the expected total for the unique digits in that section. If any of these sums don’t match $S$, the solution is invalid: $S=\sum_{i=1}^n i$ \begin{bmatrix} a_{1,1} & a_{1,2} & \dots & a_{1,n} \\ a_{2,1} & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ a_{n,1} & \dots & \dots & a_{n,n} \\ \end{bmatrix} For instance, if we represent the Sudoku grid as a matrix, we can express the sum of the elements in each column as follows: $$S=\sum_{i=1}^n a_{i, 1}$$ This summation must hold true for every row, column, and subgrid, resulting in a total of $3n$ equations, where $n$ is the size of the Sudoku grid. If any of these equations fail, it indicates an invalid solution.
These equations aren’t just random math—they form the basis of a structured verification process. In a $4 \times 4$ Sudoku, for example, you would need to verify that the sum of each row and column equals the expected total. This can be neatly packaged into a set of mathematical conditions that either confirm the correctness of the solution or point out its flaws.
Representing Verification with Arithmetic Circuits
Here’s where arithmetic circuits come into play. These circuits allow us to take the equations we’ve just discussed and represent them in a systematic way. Imagine a circuit made up of gates (like addition gates) that take inputs and produce an output. In our Sudoku example, an arithmetic circuit could be designed to verify that the sum of the numbers in a row equals $S$. If the circuit’s output matches $S$, the solution passes the test.
This isn’t just a gimmick—it’s a powerful tool. Arithmetic circuits can be designed to verify solutions to a wide variety of problems, not just Sudoku. Whether it’s checking if a number is within a certain range, proving knowledge of a discrete logarithm, or confirming a specific hash value, arithmetic circuits provide a flexible and efficient framework.
Broader Implications for Proofs of Knowledge
The ability to represent verification processes through arithmetic circuits has profound implications for zero-knowledge proofs. In these cryptographic protocols, the goal is for a prover to demonstrate they have knowledge of a solution without actually revealing the solution. By structuring the verification process through an arithmetic circuit, we can achieve this in a way that is both secure and efficient.
For example, consider a scenario where someone wants to prove they know a solution to a complex problem, like a Sudoku puzzle, without showing the solution itself. They can use an arithmetic circuit to verify the solution under the hood, and then present the verifier with the circuit’s output. The verifier is convinced that the prover knows the solution, but they never see the actual numbers on the Sudoku grid.
This method is incredibly versatile. Arithmetic circuits can be adapted to a wide range of problems, making them a cornerstone of modern cryptographic techniques. They allow us to build protocols that are not only secure but also efficient, ensuring that complex computations can be performed without compromising on performance or privacy.
References
- Frank Mangone. (2024, June 18). Cryptography 101: Commitment Schemes Revisited. Retrieved from https://medium.com/@francomangone18/cryptography-101-arithmetic-circuits-351ca87647a9
Connect with Me
Connect with me on Facebook, LinkedIn, via email at dangduongminhnhat2003@gmail.com, GitHub, or by phone at +84829258815.