Unraveling SNARKs: The Breakthrough Technology in Cryptography

Posted on: August 24, 2024 | Reading time: 20 minutes | Word count: 4201 words | Author: Dang Duong Minh Nhat

Dive deep into the fascinating world of cryptography, where proving something without revealing any secrets is not just possible—it’s essential. In this blog, we explore the intricacies of how circuit constraints are verified in SNARKs (Succinct Non-Interactive Arguments of Knowledge), ensuring that every computation is correct and secure. Whether you’re new to this topic or looking to deepen your understanding, I highly recommend checking out my previous posts: “Unveiling the Secrets of Cryptography: From Polynomials to Pairings and Commitment Schemes” and “The Math Behind the Magic: Exploring Arithmetic Circuits and Their Role in Zero-Knowledge Proofs”. These will provide you with the foundational knowledge needed to fully appreciate the advanced concepts we’ll cover here.

Table of Contents

SNARK: Unlocking the Secrets of Efficient, Private Proofs in Cryptography

In the world of cryptography, SNARKs—short for Succinct Non-interactive Arguments of Knowledge—are nothing short of revolutionary. Imagine being able to prove that you know something without revealing what it is, all while keeping the process quick and straightforward. That’s the magic of SNARKs.

What is a SNARK?

At its core, a SNARK is a cryptographic proof that allows someone (the prover) to demonstrate that they possess certain knowledge without having to share that knowledge itself. But what makes SNARKs so special? Let’s break it down:

  1. Succinctness: One of the standout features of SNARKs is their efficiency. The proof generated by a SNARK is compact, regardless of how complex the statement being proven is. This means that verifying the proof is fast and doesn’t require a lot of computational resources. Imagine being able to verify a complex computation in just seconds—SNARKs make that possible.
  2. Non-interactivity: Once the prover has created and sent the proof, their job is done. The verifier doesn’t need to interact with the prover anymore. This non-interactive nature is crucial for scenarios where continuous communication is impractical or impossible. The proof stands on its own, ready to be checked without further steps.
  3. Knowledge Proof: Perhaps the most fascinating aspect of SNARKs is their ability to prove that the prover knows something without revealing any details about that knowledge. While not all SNARKs offer this feature, those like Plonk are designed to provide zero-knowledge proofs. This means that beyond confirming the validity of the statement, no additional information is exposed—perfect for preserving privacy.

Why Do SNARKs Matter?

The unique combination of being succinct, non-interactive, and capable of preserving knowledge privacy makes SNARKs incredibly valuable in modern cryptography. They’re particularly useful in applications where privacy and efficiency are paramount, such as blockchain technologies and secure communications.

Revisiting Circuits: The Building Blocks of Efficient, Private Proofs

When it comes to proving computations without revealing sensitive information, arithmetic circuits play a crucial role. In the cryptographic world, these circuits provide a powerful way to represent complex calculations while ensuring that the prover (the person who claims to know something) doesn’t have to reveal the actual values they’re working with.

The Challenge: Proving Without Revealing

Imagine you need to convince someone that you know a secret number, let’s call it $x$, that satisfies a specific condition, but you don’t want to reveal $x$ itself. Moreover, you don’t want the verifier (the person who needs to be convinced) to go through the trouble of performing a potentially complex computation just to verify your claim. This is where arithmetic circuits come into play. $$\exists x \in \mathbb{F}_n^m / C(x, w) = 0$$

How Does It Work?

Let’s break it down. An arithmetic circuit is like a detailed recipe for a computation. It takes input values, processes them through a series of gates (like addition or multiplication), and outputs a result. The key idea here is that the prover will evaluate this circuit and record the entire process in a structured way, known as a computation trace.

Think of this trace as a table that logs every step in the computation:

  • Inputs: The initial values you start with.
  • Gates: The operations performed on these values.
  • Outputs: The results of these operations.

Line Source Image

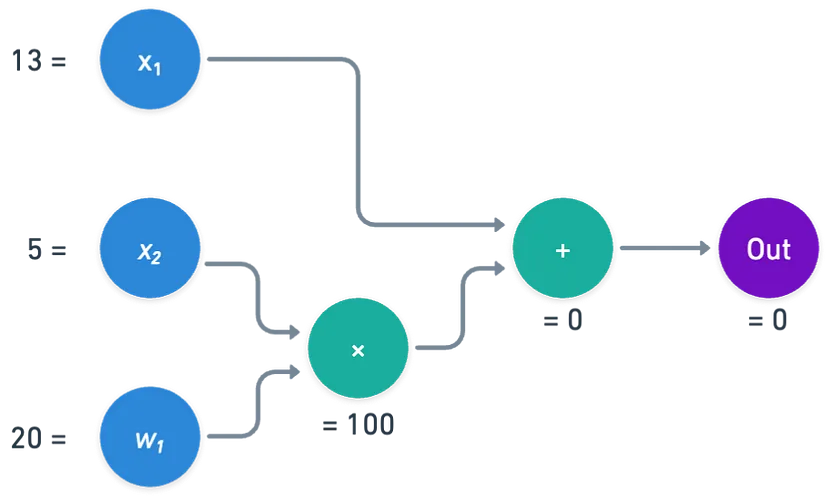
For example, consider a simple evaluation using a finite field (think of it as a special kind of arithmetic) with modulo $n = 113$:

+-----------+------+------+------+
|           |  w1  |  x1  |  x2  |
+-----------+--------------------+
| inputs    |  20  |  13  |  5   |
+-----------+--------------------+

+-----------+--------------+---------------+----------+
|           |  left input  |  right input  |  output  |
+-----------+--------------+---------------+----------+
| gate 0    |  5           |  20           |  100     |
+-----------+--------------+---------------+----------+
| gate 1    |  13          |  100          |  0       |
+-----------+--------------+---------------+----------+

Here, you see the inputs, the operations at each gate, and the outputs.

The Power of Polynomials

Modern SNARKs, like Plonk, take this concept a step further by encoding the entire computation trace into polynomials. This encoding allows the verifier to easily check if the computation was performed correctly without needing to see the actual numbers.

Here’s how it works:

  1. Gate Evaluation: The verifier checks if each gate was evaluated correctly according to the rules of the circuit.
  2. Wire Consistency: The values on wires (connections between gates) must be consistent, especially if they share a common source. For example, certain wires should carry identical values to maintain consistency across the circuit.

In simpler terms, the circuit not only performs the computation but also sets up a series of checks to ensure everything is correct. Each of these checks is represented by a different polynomial, and the entire computation is captured by a single polynomial $P$.

Line Source Image

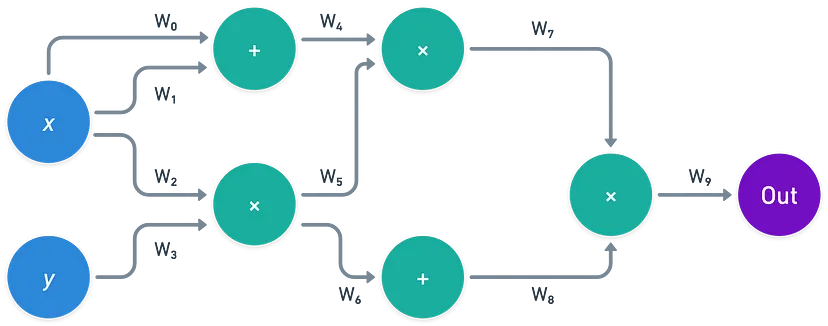
For example, in a circuit, certain wires should hold the same value (e.g., $W_0, W_1​$, and $W_2$ should be identical, as well as $W_6​$ and $W_5$). Additionally, gate operations should be consistent (e.g., $W_0+W_1$ should equal $W_4$).

In this context, a circuit serves as both a recipe for computation and a set of constraints to verify. Each set of constraints — including wire values, gate operations, and wiring constraints — is encoded into different polynomials. The entire computation trace can be represented by a single polynomial $P$, where $P\left(x_i\right)$ corresponds to a specific wire value.

Roots of Unity: The Secret Sauce Behind Efficient Proofs

In the world of cryptography, roots of unity might sound like a mysterious concept, but they play a crucial role in making complex computations both efficient and elegant. Let’s dive into what they are and why they’re so powerful.

What Are Roots of Unity?

Imagine you have a special number, represented by the Greek letter omega ($\omega$), that has a magical property: when you multiply it by itself a certain number of times, it brings you back to 1. For example, if $\omega$ is a $k$-th root of unity, then: $$\omega^k = 1 (\text{mod }p)$$ This means that if you keep multiplying $\omega$ by itself, after $k$ steps, you end up back where you started—at 1. The set of these numbers (including 1) forms what’s known as a cyclic group. This group, denoted as $H$, is made up of the numbers:

$H =$ {$1, \omega, \omega^2, \dots, \omega^{k - 1}$}

Why Are Roots of Unity So Useful?

When we’re working with polynomials—an essential part of SNARKs (Succinct Non-interactive Arguments of Knowledge)—we need to encode values efficiently. Here’s where roots of unity come in handy:

Efficient Movement Through Values

One of the coolest things about roots of unity is how easy it is to move from one value to the next. To transition from $\omega$ to $\omega^2$, you just multiply by $\omega$. To go backward, you multiply by the inverse of $\omega$. This cyclical nature makes navigating through the set incredibly straightforward and efficient.

For example, because the group is cyclic, you can always return to the starting point: $$\omega^{k - 1} \times \omega = 1 \text{ and } \omega^{-1} = \omega^{k - 1}$$

Speedy Calculations with Fast Fourier Transform (FFT)

But the real magic happens when we talk about interpolation—the process of finding a polynomial that passes through a given set of points. Normally, this could be a slow and cumbersome task, but using roots of unity allows us to use the Fast Fourier Transform (FFT), a super-efficient algorithm that speeds up the entire process.

FFT is like the turbocharger of polynomial interpolation. By leveraging the cyclical nature of roots of unity, FFT can compute the necessary polynomials in a fraction of the time it would take using other methods. This efficiency is key in cryptographic applications, where speed and accuracy are paramount.

Encoding the Circuit: How Plonk Keeps Everything in Check

In the cryptographic world, ensuring that every part of a computation is accurate and secure is crucial. One way to do this is through a process called encoding, which translates the steps of a computation into a format that can be easily checked. Let’s explore how this works, particularly in the context of Plonk, one of the most advanced cryptographic protocols today.

The Basics of Encoding: What Are We Working With?

When we talk about encoding a circuit, we’re essentially breaking down a complex computation into manageable pieces and then representing those pieces in a mathematical way. Imagine you have a circuit with a certain number of inputs and gates (the building blocks that perform operations like addition and multiplication). To keep things organized, we need to define a critical value, which we’ll call $d$. This value determines how many elements (inputs, outputs, and intermediate results) we need to track throughout the computation.

Here’s how we calculate it: $$d = 3|C| + |I|$$ Where:

  • $|C|$ is the number of gates.
  • $|I|$ is the number of inputs.

Each gate has three associated values: two inputs and one output. The total number of elements in our computation trace is represented by $d$. Once we have this value, we can start encoding.

These values will be encoded into the $d$-th roots of unity:

$H =$ {$1, \omega, \omega^2, \dots, \omega^{d - 1}$}

Mapping the Circuit to Roots of Unity

The mapping of roots to specific wires in the circuit requires a systematic approach. The inputs $|I|$ are encoded using the negative powers of $ω$. For the $j$-th input, we use: $$P\left(\omega^{-j}\right)$$ For each gate $k$, which has three associated wires (left input, right input, and output), the encoding is defined as: $$P\left(\omega^{3k}\right), P\left(\omega^{3k+1}\right), P\left(\omega^{3k + 2}\right)$$ This systematic encoding ensures that all values in the computation trace are included in the polynomial. Once these values are encoded, the next step is to interpolate them to obtain the polynomial $P(x)$ of degree $d-1$.

Handling Different Types of Gates

Gates in the circuit can be either addition or multiplication gates, and encoding their operation requires distinguishing between these types. To achieve this, we use a selector polynomial $S(x)$. For a gate $k$: $$S\left(\omega^{3k}\right) = 0 \text{ or } S\left(\omega^{3k}\right) = 1$$ $$S\left(x_k\right) =$$ \begin{cases} 1 \text{ if the gate is an addition gate,} \\ 0 \text{ if the gate is an multiplication gate.} \end{cases} This polynomial $S(x)$ allows us to construct an expression that links the inputs and outputs of each gate: $$S(\alpha)[P(\alpha) + P(\omega \alpha)] + (1 - S(\alpha))P(\alpha)P(\omega \alpha) - P\left(\omega^2 \alpha\right) = 0$$ This expression ensures that only the relevant term (either addition or multiplication) is active for each gate $k$, depending on its type, and thereby verifies the correct evaluation of the gate.

Wiring Encoding: Ensuring Everything Matches Up

The wiring constraints are perhaps the most complex part of the encoding process. These constraints ensure that certain wires, which originate from the same source, hold the same value throughout the circuit.

Line Source Image

For example, if we have wires that should hold the same value: $$P\left(\omega^p\right) = P\left(\omega^q\right) = P\left(\omega^r\right) = P\left(\omega^s\right)$$

We define a subset of roots $H^{’}$ such that:

$H^{’} =$ {$\omega^p, \omega^q, \omega^r, \omega^s$}

We then construct a permutation polynomial $W(X)$ that cyclically maps these roots to each other:

$$ W\left(\omega^p\right) = \omega^q \\ W\left(\omega^q\right) = \omega^r \\ W\left(\omega^r\right) = \omega^s \\ W\left(\omega^s\right) = \omega^p $$

The wiring constraint is satisfied if: $$P(x) = P(W(x)) \forall x \in H^{’}$$

This condition must hold for every element in $H^{’}$, effectively ensuring that the values across all corresponding wires are equal.

This method of wiring encoding is a key component of the Plonk protocol, and it is what gives Plonk its flexibility in proving that the entire circuit satisfies the required constraints.

Verification in Plonk: Ensuring Trust Without Revealing Secrets

When it comes to cryptographic proofs, one of the most fascinating challenges is how to convince someone that a computation is correct—without giving away any secret information. This is where protocols like Plonk shine, offering powerful ways to verify complex computations while maintaining absolute privacy. Let’s break down how this works, focusing on the verification process.

The Art of Verification: Protecting Secrets

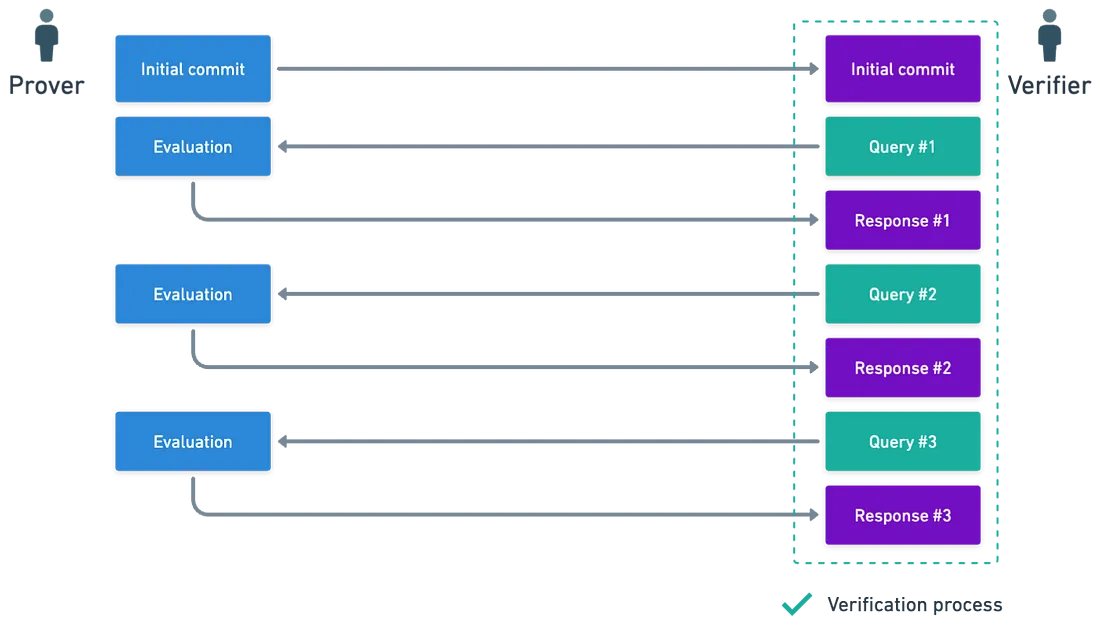
In the world of Plonk, we deal with polynomials—special mathematical expressions that help encode all the steps of a computation. However, it’s crucial that these polynomials, especially the main one we’ll call $P(X)$, remain hidden from the verifier (the party checking the proof). Why? Because if the verifier could see the full polynomial, they might figure out the secret input values, which defeats the whole purpose of privacy. If the verifier were to obtain the full polynomial, they could potentially uncover the secret information $x$ by calculating: $$P\left(\omega^{-j}\right)$$ If the verifier cannot know the full polynomials, how can they be convinced that the computation is correct? While the verifier cannot access the complete polynomials, they can request single evaluations of these polynomials. Specifically, they can query the value of $P(X), S(X)$, or the wiring polynomials $W(X)$ at any given point, without revealing the secret inputs.

Querying Polynomials: A Peek Without the Full Picture

Imagine you’re trying to verify a complex computation. You don’t need to see every detail—you just need to check certain key points. In Plonk, the verifier can ask for the value of a polynomial at a specific point, say $P(b)$, without ever seeing the rest of $P(X)$. This is possible thanks to Polynomial Commitment Schemes (PCS).

Here’s how it works:

  1. Commitments: The prover (the party creating the proof) generates a commitment to the polynomial. This commitment acts like a seal that’s impossible to fake.
  2. Queries: The verifier asks for the value of $P(X)$ at a particular point, say $b$.
  3. Verification: The prover reveals this single value, and the verifier checks it against the commitment. If it matches, the verifier can be confident that the entire polynomial (and thus the computation) is correct.

This method allows the verifier to check the computation without ever seeing the full polynomial, keeping the secret inputs safe.

The Essential Checks: What Must Be Verified?

To ensure everything is correct, the verifier needs to check several key aspects of the computation:

  1. Final Output Check: The output of the last gate in the circuit should be exactly zero. This confirms that the computation ended correctly.
  2. Input Encoding Check: The public inputs (or witnesses) must be encoded correctly. This ensures that the inputs to the circuit match what was expected.
  3. Gate Evaluation Check: The operations performed by each gate—whether it’s addition or multiplication—must be accurate. This confirms that the computation itself was done correctly.
  4. Wiring Check: The wires connecting different parts of the circuit must hold consistent values throughout. This ensures that the data flows correctly from one part of the circuit to another.

These checks are vital for verifying the integrity of the entire computation.

The first check is straightforward; the verifier simply requests the output at the last gate, which should be: $$P\left(\omega^{3|C| - 1}\right) = 0$$ The remaining checks involve more complex processes, requiring additional cryptographic techniques.

Zero Tests: The Secret Sauce of Verification

To ensure the correctness of polynomials, we use a concept known as a zero test. Given a polynomial $f(X)$ of degree at most $d$ (which is not identically zero), the probability that a randomly chosen input $r$ will satisfy $f(r)=0$ is: $$P[f(r) = 0] \leq d/n$$ Here, $n$ is the modulus, and if n is sufficiently larger than $d$, the probability of $f(r)=0$ becomes negligible. If a random $r$ indeed results in $f(r)=0$, we can be highly confident that $f(X)$ is identically zero, meaning that the constraints are satisfied.

This zero test forms the foundation of the verification process in SNARKs, ensuring that the verifier can trust the correctness of the proof without needing to access the full polynomials.

Understanding Interactive Oracle Proofs (IOPs): The Backbone of Secure Cryptographic Verification

In the fascinating world of cryptography, one of the biggest challenges is proving that something is true without revealing any secrets. This is where Interactive Oracle Proofs (IOPs) come into play. IOPs form the foundation of many cryptographic protocols, enabling a prover to convince a verifier of a particular statement’s truth—without giving away any sensitive information. Let’s explore how this process works and why it’s so crucial.

What Are Interactive Oracle Proofs (IOPs)?

At its core, an IOP is a way for two parties—the prover and the verifier—to interact in such a way that the verifier can be confident in the truth of a statement. Imagine a conversation where one person is trying to convince the other that a particular set of facts is correct. In cryptographic terms, this interaction ensures that the prover is being truthful, while the verifier remains secure, never learning more than they need to.

Line Source Image

Interactive Oracle Proofs are similar to Polynomial Commitment Schemes (PCSs), where the interaction is structured to be both efficient and secure. This setup ensures that even though the prover and verifier are exchanging information, the process remains private and safe.

A Simple Example: The Zero Test with IOPs

To see IOPs in action, let’s look at a simple example called the Zero Test. Suppose a prover wants to show that a specific set $S =$ {$s_0, s_1, …, s_{n -1}$} consists of the roots of a polynomial $P(X)$. The key tool here is the vanishing polynomial $V(X)$, which equals zero exactly at the roots in $S$. $$V(X) = \prod_{i = 0}^{n - 1}\left(X-s_i\right)$$ The prover’s goal is to demonstrate that when $P(X)$ is divided by $V(X)$, the result is a quotient $Q(X)$ with no remainder. If this division holds true, it confirms that $S$ is indeed the set of roots for $P(X)$. $$Q(X) = P(X)/V(X)$$ Here’s how it works:

  1. Commitments: The prover starts by committing to both $P(X)$ and $Q(X)$ using a Polynomial Commitment Scheme. This means that the prover creates a secure “commitment” to these polynomials, much like sealing an envelope that only the verifier can later open.
  2. Queries: The verifier then requests the value of $P(X)$ and $Q(X)$ at a random point $s_i$ from the set $S$. This randomness ensures that the prover can’t cheat.
  3. Verification: The verifier checks whether the following equation holds true: $$Q\left(s_i\right).V\left(s_i\right) - P\left(s_i\right) = 0$$ If this equation is satisfied for the randomly chosen point $s_i$, the verifier can confidently conclude that $S$ is indeed the set of roots of $P(X)$.

Line Source Image

This process is powerful because it allows the verifier to be convinced without needing to see the entire polynomials. And if the verifier wants even more confidence, they can ask for additional evaluations at different points.

Similar IOPs are employed for other checks, such as the addition check and the product check. It is important to note, however, that this method does not guarantee that there are no other roots of $P(X)$ outside of $S$.

From Interactive to Non-Interactive Proofs

While IOPs are inherently interactive, many cryptographic protocols, such as SNARKs (Succinct Non-Interactive Arguments of Knowledge), are designed to be non-interactive. So, how do we bridge this gap?

The solution lies in a clever technique called the Fiat-Shamir Transformation. This transformation is a cryptographic trick that turns an interactive proof into a non-interactive one.

In an interactive setting, the verifier generates random numbers during the verification process, which keeps the prover on their toes. The Fiat-Shamir Transformation replaces this need for back-and-forth communication by using a cryptographic hash function to simulate randomness. Essentially, the prover hashes certain parts of the proof to generate the required random values, ensuring the proof’s integrity without needing to interact with the verifier directly.

This transformation is a game-changer in cryptography because it allows for secure, non-interactive proofs that are just as reliable as their interactive counterparts.

Ensuring Trust in Cryptographic Circuits: A Deep Dive into Circuit Constraint Verification

When it comes to cryptographic proofs, one of the most critical steps is verifying that a circuit’s constraints are properly upheld. This verification ensures that the prover knows a secret value, say $x$, that satisfies all the rules of the circuit. In this post, we’ll break down the process of verifying these constraints into three key aspects: the correctness of inputs, gate computations, and wiring. Let’s dive in!

Correctness of Inputs: Setting the Stage

The first step in this verification journey is to ensure that the inputs provided by the prover are correct. The verifier, who acts as the “judge,” already knows a public witness $w$—a value that’s shared and agreed upon. The verifier’s job is to encode this witness into a polynomial $v(X)$ in such a way that: $$v\left(\omega^i\right)=w_i \text{ (where } w_i \text{ is the public witness)}$$ But what does this mean in practice?

For the circuit to be valid, the values of $v(X)$ and $P(X)$ (which encodes the computation trace of the circuit) must match at specific points, called the roots of unity, that correspond to the public witness. This can be expressed as: $$v\left(\omega^i\right) = P\left(\omega^i\right) \text{ for each root }\omega^i$$ Here, $\omega^i$ represents these special points, and $P(X)$ represents the polynomial that traces the entire computation.

To verify this, the verifier performs a zero test. This test checks if $P(X)- v(X)$ is zero at these specific points. If the test comes back zero, it’s a green light—the inputs are correctly encoded!

Correctness of Gate Computations: Checking the Circuit’s Math

Next up, we need to ensure that each gate (the basic building block of our circuit) is functioning as it should. Whether a gate is adding, multiplying, or performing some other operation, it must adhere to the following rule: $$S(\alpha)[P(\alpha) + P(\omega \alpha)] + (1 - S(\alpha))P(\alpha)P(\omega \alpha) - P\left(\omega^2 \alpha\right) = 0$$ , where $\alpha = \omega^{3k}$

Here, $S(X)$ is known as the selector polynomial. It tells us what type of operation each gate is supposed to perform—whether it’s an addition gate, a multiplication gate, or something else.

To confirm that each gate is doing its job correctly, the verifier runs a zero test on this expression for every gate in the circuit. This step ensures that all the mathematical operations encoded in the circuit are accurate. The prover helps by providing a commitment to the polynomial $S(X)$, which makes the verification process smooth and efficient.

Correctness of Wiring: Ensuring the Circuit Stays Connected

Finally, we need to verify the wiring—the invisible connections that ensure the circuit’s structure remains intact. Think of the circuit as a complex puzzle, where each piece must fit perfectly with the others. These wiring constraints are encoded into polynomials $W(X)$, which essentially shuffle (or permute) elements of a set $H^{’}$.

The goal is to ensure that $P(x) = P(W(x)) \forall x \in H^{’}$. Instead of performing another zero test here, which could be cumbersome, we use something called a product check. The expression to verify looks like this: $$L(Y,Z) = \prod_{x \in H^{’}} \frac{P(x) + Y.W(x) + Z}{P(x)+Y.x+Z}$$ The gist of this is that the whole expression should equal 1! If you think about it, it makes perfect sense: all the $P(x)$ values should be the same, and since $W(X)$ permutates the elements of $H^{’}$, and because the product covers all of $H^{’}$, we just get: $$L(Y,Z) = \prod_{x \in H^{’}} \frac{P(x) + Y.W(x) + Z}{P(x)+Y.x+Z} = \frac{\prod_{x \in H^{’}} P(x) +Y.W(x) + Z}{\prod_{x \in H^{’}}P(x)+Y.x+Z}$$ $$= \frac{\prod_{x \in H^{’}} P(x) +Y.x + Z}{\prod_{x \in H^{’}}P(x)+Y.x+Z} = 1$$

References

  1. Frank Mangone. (2024, June 25). Cryptography 101: Zero Knowledge Proofs (Part 2). Retrieved from https://medium.com/@francomangone18/cryptography-101-zero-knowledge-proofs-part-2-9e14467ed0be

Connect with Me

Connect with me on Facebook, LinkedIn, via email at dangduongminhnhat2003@gmail.com, GitHub, or by phone at +84829258815.

Cryptography  Zero-Knowledge Proofs  SNARKs  Commitment Schemes  Interactive Oracle Proofs  Arithmetic Circuits